Таблица умножения за 3 дня. Как запомнить таблицу умножения за 3 дня, при этом не зубрить её

Таблица умножения за 3 дня. Как запомнить таблицу умножения за 3 дня, при этом не зубрить её
Станислав Баранов

В книге описана методика заучивания таблицы умножения за 3 дня без использования способа зубрёжки. Книга написана для родителей учеников младших классов и для школьников, изучающих таблицу умножения самостоятельно.

Таблица умножения за 3 дня

Как запомнить таблицу умножения за 3 дня, при этом не зубрить её

Станислав Баранов

© Станислав Баранов, 2016

ISBN 978-5-4483-3755-0

Создано в интеллектуальной издательской системе Ridero

Введение

Цель этой книги научить детей таблице умножения за 3 дня, не мучая их зубрежкой. Книга написана как для родителей, которые хотят, чтобы дети знали таблицу умножения, но при этом не зубрили её, так и для детей, которые уже могут самостоятельно читать и учат таблицу умножения самостоятельно.

Из опыта нашего образования[1 - образования – я его называю «обрезавание» – она обрезает творческие способности детей и делает их винтиками нашей системы] дети учат таблицу умножения в зависимости от способностей в среднем от 6 месяцев до 1 года. Представленная методика позволяет сократить обучение таблице умножения за 3 дня начать обучение в пятницу вечером и закончить в воскресение вечером. При этом никаких психологических травм: «Математика очень трудный предмет – математика не для меня».

На моей практике встречались разные дети – как с математическим складом ума (такие учили таблицу умножения по методике за 1 день), так и «лирики» – такие радостно узнавали, что математика одно удовольствие и учили таблицу за три дня. В методике зазубрить придется всего 10 примеров.

Я не приписываю авторство данного метода себе – я просто записал уже известное в печатном виде.

Как выглядит таблица умножения и как ей пользоваться

Никогда не используйте таблицу умножения, которая выглядит как много строк. В ней ничего не понятно для ребенка и только отпугивает его: он подсознательно будет стремится отложить запоминание на другой срок.

Рисунок 1. Неправильная таблица умножения-не используйте такую

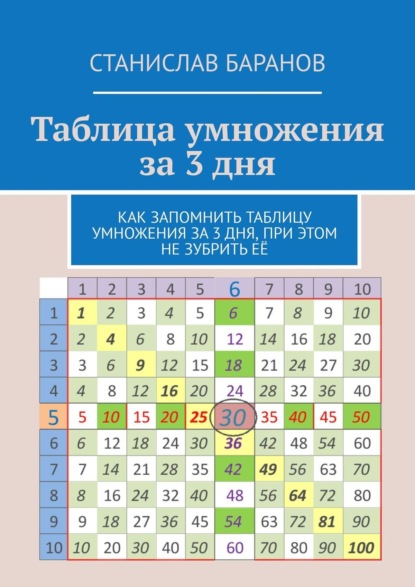
«Какую же таблицу надо использовать?» – спросит читатель. Использовать надо таблицу умножения в таком виде, так называемой таблицей Пифагора:

Рисунок 2. Таблица Пифагора

Автор немного раскрасил таблицу, чтобы ещё больше подчеркнуть её простоту и гениальность.

Рисунок 3. Раскрашенная таблица Пифагора.

Как пользоваться данной таблицей? Чтобы узнать результат умножения двух чисел, надо найти клетку пересечения строки первого числа со столбцом второго числа (можно и наоборот, так как результат не поменяется).

Рисунок 4. Результат умножения 5*6=30

Как уже, наверное, заметили, результат умножения 6*5 будет тоже 30-

5*6=6*5=30

День первый

Умножение на 1

Рисунок 5. Умножение на 1.

Правило.

Произведение какого-либо числа на 1 будет равняться этому же числу.

Для того, чтобы умножить на 1, надо просто назвать число, которое умножали на 1.

Рисунок 6. Правило УМНОЖЕНИЕ НА 1.

Таким образом, умножение на 1 учить не надо. Следовательно, из нашей таблицы 10 на 10 (будет 100) нужно вычесть 19 примеров умножения на 1. В таблице зеленым цветом выделены произведения, которые «выучили». Осталось выучить 81 пример (в таблице они выделены черным цветом).

Рисунок 7. Таблица умножения после изучения умножения на 1.

Умножение на 2

В таблице примеры умножения выделены синим цветом.

Рисунок 8. Таблица Пифагора с примерами умножения на 2 (синим цветом)

Выпишем все эти примеры:

Рисунок 9. Примеры умножения на 2.

Правило умножения на 2.

Для того, чтобы умножить на 2, складываем второй сомножитель с самим собой. Таким образом, умножение заменяем сложением.

Следовательно, опять ничего не нужно учить.

Рисунок 10. Правило умножения на 2.

Здесь применяем правило – человек легче и быстрее складывает, чем умножает. Недаром сложение и вычитание действия первого порядка, умножение и деление – действия второго порядка. Несколько столетий назад человека, который мог делить, считали очень умным (как минимум профессор своего времени).