
Особенности расчета дифференциального высокочастотного фильтра

Владимир Шлома, Сергей Макаров
Особенности расчета дифференциального высокочастотного фильтра
1
Краткий анализ существа вопроса
При проектировании специализированного цифрового радиоприемного устройства, предназначенного для контроля параметров излучений базовых и абонентских станций ТЕТРА, встала задача расчета электрической схемы фильтров нижних частот, имеющих дифференциальные вход и выход.
Теория и практика расчета высокочастотных фильтров проработаны очень глубоко [1 – 5], кроме того в интернете достаточно много программ по расчету фильтров, таких как RFSm99, которые, после подстановки исходных данных для расчета, позволяют сразу получить достаточно точный результат вычислений. Никаких трудностей в решении этой задачи не предвиделось.
Однако, простая, на первый взгляд, задача оказалась не очень простой. Нам не удалось найти каких-либо теоретических разработок или практических рекомендаций по расчету именно дифференциальных фильтров. Во всех доступных нам источниках, в том числе и программах, рассматриваются вопросы расчета простых (без дифференциального входа/выхода) фильтров.
Задачу расчета фильтра с дифференциальным входом/выходом пришлось решать самостоятельно. При решении задачи были рассмотрены два варианта преобразования схемы обычного фильтра в дифференциальный.
2
Первый вариант преобразования
Схема обычного фильтра нижних частот показана на рис. 1.

Рисунок 1. Схема простого фильтра нижних частот
Фильтр состоит из двух элементов: L и C. Входное сопротивление Rвх и выходное сопротивление фильтра Rвых показаны на схеме условно. Фильтр подключается к некоторому источнику с выходним сопротивлением Rи. К выходу фильтра подключается нагрузка Rн. При расчете фильтра обязательно должны быть согласованы входное и выходное сопротивления фильтра: Rвх=Rи, Rвых=Rн.
Для создания дифференциального фильтра был предложен наиболее простой вариант: собрать дифференциальный фильтр из двух одинаковых обычных, как показано на рис. 2.
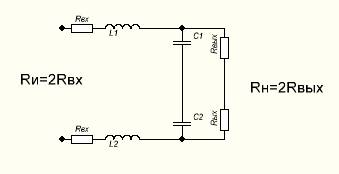
Рисунок 2. Объединение двух простых фильтров
На рис. 2 номиналы элементов связаны с рис. 1 следующими соотношениями: L1=L2=L, С1=С2=С.
Из рисунка 2 видно, что полученный фильтр не согласован по сопротивлениям. Входное и выходное сопротивление фильтра в два раза больше требуемого. Для того, чтобы согласовать сопротивления, при расчете одного плеча фильтра (простого фильтра) нужно исходить из условия: Rвх=Rи/2, Rвых=Rн/2. Фильтр нужно пересчитать исходя из новых условий. При пересчете получим новые значения номиналов L и С. Конденсаторы С1 и С2 можно заменить одним конденсатором С1. Поскольку С1=С2=С, то емкость нового конденсатора С1 должна быть С/2. Окончательная схема дифференциального фильтра приведена на рис. 3.
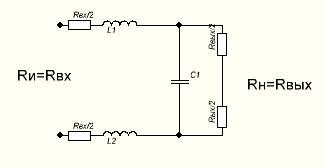
Рисунок 3 Схема согласованного дифференциального фильтра
Теперь дифференциальный фильтр будет согласованным по сопротивлениям и иметь требуемую амплитудно-частотную характеристику.
Аналогично по схеме рис.3 можно преобразовывать в дифференциальные и более сложные фильтры. При этом нужно соблюдать следующие правила:
1. расчет элементов обычного фильтра производить исходя из условия: Rвх=Rи/2, Rвых=Rн/2;
2. элементы, включенные в фильтре последовательно, имеют те же номиналы, которые были получены при расчете обычного фильтра;
3. элементы, включенные в фильтре параллельно, нужно пересчитать. Номинал индуктивностей нужно увеличить в 2 раза, а номинал конденсаторов уменьшить в 2 раза по отношению к рассчитанным для обычного фильтра.
3
Второй вариант преобразования
Второй вариант заключается в последовательном преобразовании схемы обычного фильтра по известным в теории фильтров правилам.
Поскольку дифференциальный фильтр не имеет соединений с корпусом, в схеме фильтра рис.1 уберем все соединения с корпусом. Получим схему обычного фильтра, представленную на рис.4.
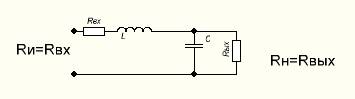
Рисунок 4. Обычный фильтр
Как видно из рис. 4 это Г-образный фильтр. Преобразуем его в Т‑образный фильтр, используя известные [1, 2, 4] правила: включенные последовательно катушки индуктивности и конденсаторы разбиваются на два с номиналами L1=L2=L/2, C1=C2=2C, элементы, включенные параллельно, не изменяются. В результате таких преобразований получим схему, представленную на рис.5.
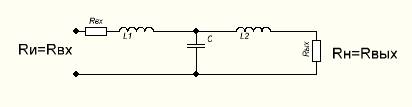
Рисунок 5. Т-образный фильтр
Получили Т-образный фильтр, по своим характеристикам эквивалентный приведенному на рис.4. Номиналы катушек индуктивности L1=L2=L/2.
Переместим катушку индуктивности L2 по цепи протекания тока в нижнее плечо, таким образом, чтобы величина протекающего в цепи тока не изменилась. Условно показанное на схеме рис. 5 входное сопротивление Rвх разобьем на два с номиналами Rвх/2 и одно перенесем в нижнее плечо. В результате получаем схему согласованного дифференциального фильтра, приведенную на рис. 6.
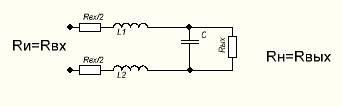
Рисунок 6. Дифференциальный фильтр
На рис. 6 номиналы элементов связаны с рис. 4 следующими соотношениями: L1=L2=L/2, номинал конденсатора не изменился.
Аналогично по схеме рис.6 можно преобразовывать в дифференциальные и более сложные фильтры. При этом нужно соблюдать следующие правила:
1. расчет элементов обычного фильтра производить исходя из условия: Rвх=Rи, Rвых=Rн;
2. элементы, включенные в фильтре параллельно, имеют те же номиналы, которые были получены при расчете обычного фильтра;
3. элементы, включенные в фильтре последовательно, нужно пересчитать. Номинал индуктивностей нужно уменьшить в 2 раза, а номинал конденсаторов увеличить в 2 раза по отношению к рассчитанным для обычного фильтра.
Практическая реализация дифференциальных фильтров, рассчитанных по первому и второму способу показала, что их параметры и характеристики, с достаточной для практического применения точностью, соответствуют расчетным. Поэтому оба предложенные варианта преобразования обычных фильтров в дифференциальные могут применяться при решении практических задач.
Литература
1. Босый Н.Д. Электрические фильтры. – УССР: ГИТЛ, 1957 – 516 с.
2. Белецкий А.Ф. Основы теории линейных электрических цепей. – М.: Связь, 1967 – 206 с.
3. Альбац М.Е. Справочник по расчету фильтров и линий задержки. – М.: ГТИ, 1963 – 200 с.
4. Ханзел Г. Справочник по расчету фильтров/ Пер. с англ.; Под ред. А.Е. Знаменского. – М.: Советское радио, 1974 – 288 с.
5. Зааль Р. Справочник по расчету фильтров/ Пер. с нем.; Под ред. Н.Н. Слепова. – М.: Радио и связь, 1983 – 751 с.


