
Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.
Квинта должна была сохранить свою чистоту – остаться чистой квинтой.
И отразиться чистой квартой.
Это возможно только в том случае, если и расстояния между звуками будут подобны квинте.
И в самом деле, взгляни на знакомую таблицу, – и ты увидишь, что звуки с их высчитанными частотами словно сами собой распределились по расстояниям в соответствии с квинтой: два тона – три тона. 2/3. По длине волны квинты.
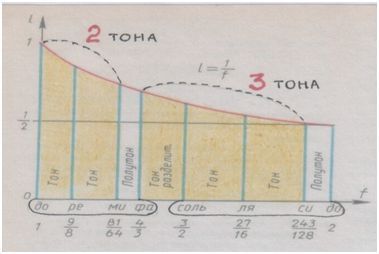
Рис. автора.
А оставшийся ш е с т о й тон стал границей, разделом, – сам поделившись надвое.
Сами звуки расположились симметрично, по квартам. А расстояния между ними – асимметрично, по квинтам.
Симметрия и асимметрия – в одном.
Симметрия и асимметрия в одной октаве.
Симметрия и асимметрия в отрезке (октава – интервал, интервал – отрезок).
Быть может, ты вспомнишь, где нам встречалось это явление: сочетание симметрии и асимметрии вместе?
… «ДЕЛЕНИЕ ОТРЕЗКА В КРАЙНЕМ И СРЕДНЕМ ОТНОШЕНИИ»…
…Ну, конечно же… Золотое сечение!

Рис. автора.
Но вместе всё это сотворяет особую симметрию – САМОПОДОБИЕ.

Рис. автора
Геометрические мысли о консонансах.

Модель автора

Рис. и пометки автора.
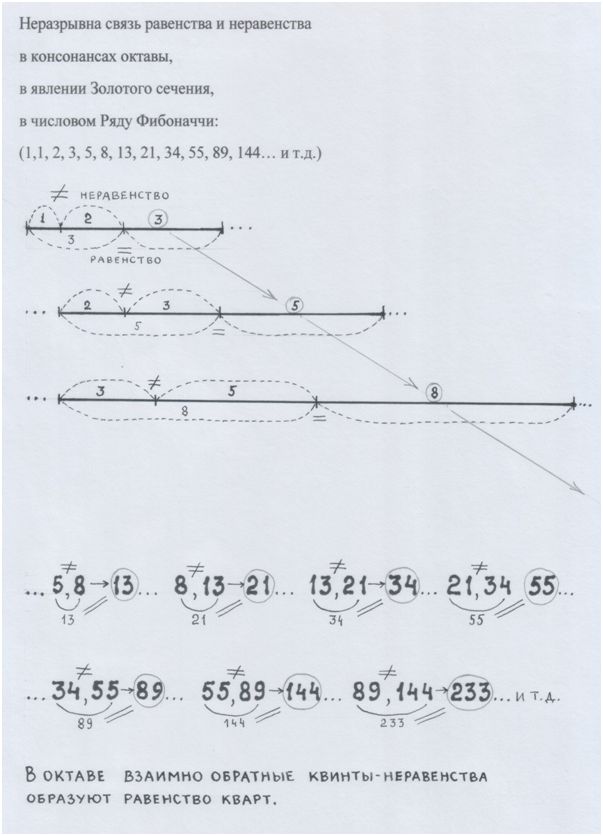
Рис. и пометки автора.
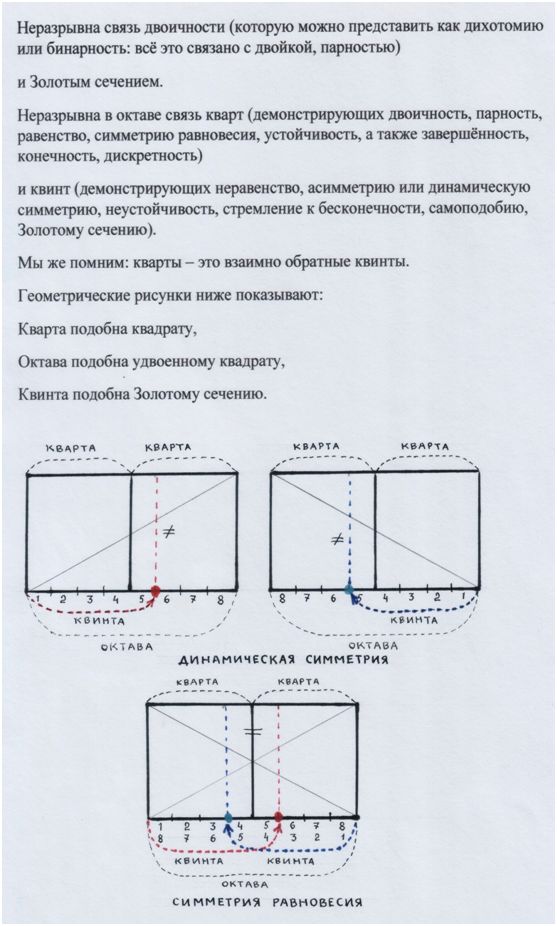
Рис. и пометки автора.
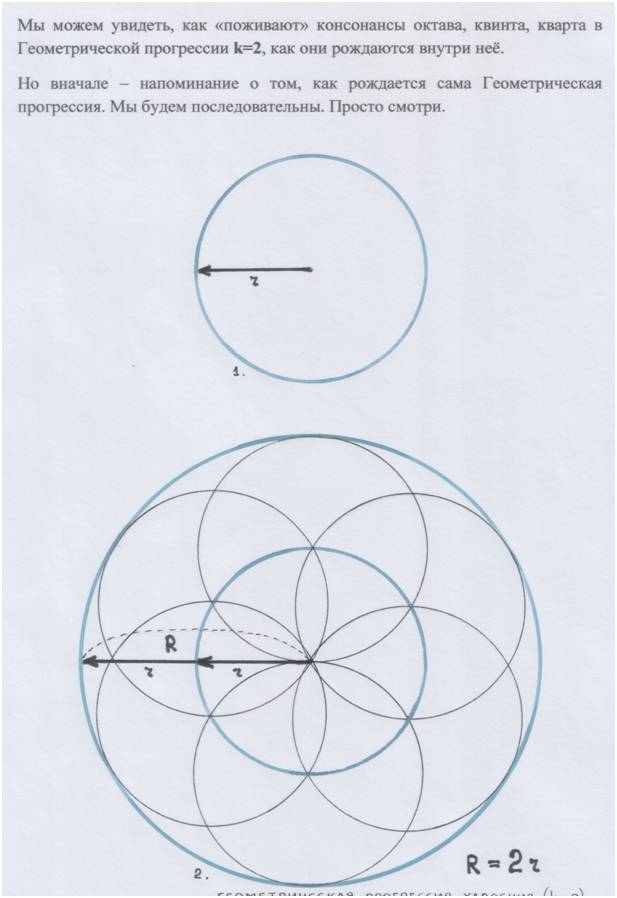
Рис. и пометки автора.
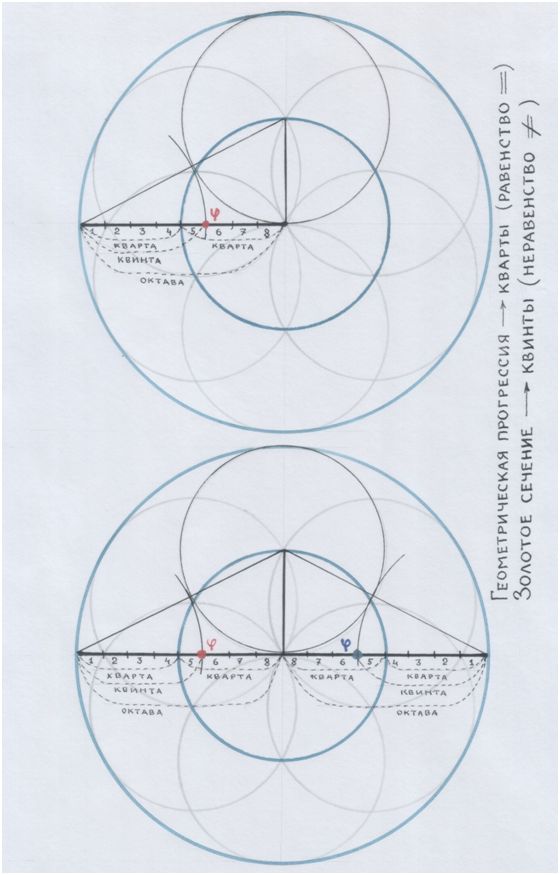
Рис. и пометки автора.
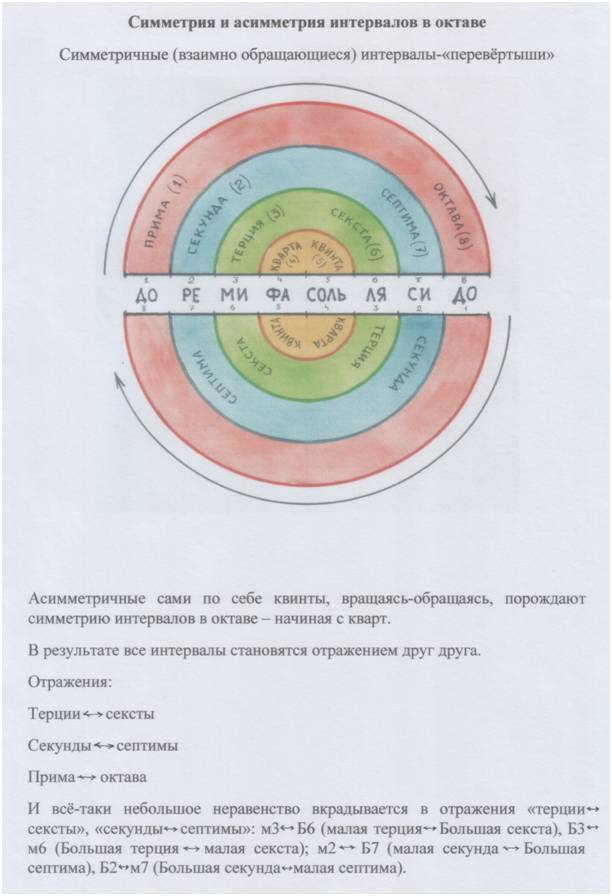
Рис. и пометки автора.
…Ох, это Золотое сечение! Куда ни взглянешь – машет ручкой: привет-привет! А уж на клавишах так прямо само в глаза бросается: вот оно я! Вот же!
Как же Пифагор обходился без клавиш?
Ну не было их тогда. Вместо клавиш – геометрия! Отрезки, пропорции, числа-дроби.
Вот и та, последняя, таблица, с интервалами-отрезками между звуками октавы… Мы в ней далеко не всё интересное разглядели и обмыслили.
Слово там одно необычное не даёт покоя.
Ты видишь его, это слово?

Рис. автора.
…ЛИММА.
Зачем здесь такое странное слово?
Странное. Но какое красивое!
Греческое.
А означает – «остаток». Всего лишь! Так просто…
Однако греки и любили-то именно сочетание простоты и красоты.
Ну сравни сам, вслушайся: «полутон» и … Лимма, Леймма… Это же музыка!
Даже в простом слове – музыка.
Энциклопедия:
Ли́мма (устар. ле́ймма) (греч. λεῖμμα – остаток, лат. limma, реже leimma) – музыкальный интервал, соответствующий диатоническому полутону (малой секунде) пифагорова строя. Согласно античному определению, восходящему к пифагорейской школе, лимма равна разности чистой кварты и двух целых тонов (отсюда название как «остатка» кварты после отделения от неё двух целых тонов) и, таким образом, имеет отношение частот верхнего и нижнего звука, равное
4/3 : (9/8)² = 256/243
Не думаю, что оставшиеся странички этой тетради ты бы (вдруг!) прочитал «взахлёб». Они сухи, как осенние листья, как древние папирусы. Царапины Истории. В них не ощущается той жгучей эмоции, которая воспламеняет любопытство и азарт следователя, напавшего на след тайны. А ведь изначально было именно так! У Платона, у Боэция, и ещё у многих. Они – и тайна Пифагора. И благодаря им мы тоже теперь причастны этой тайне. И тоже – будто следователи. Увлечены.
Пламя притушено, эмоции высушены «учёным стилем» и временем. Просто исторические документы. И даже – всего лишь какие-то лоскутки текстов в этих документах.
Хочешь – взгляни. А вдруг у тебя получится угадать за этим – п о и с к.

«Афинская школа» Рафаэля. Фрагмент. Пифагор.



Звуки под микроскопом и в телескоп. Продолжение истории о молотках и наковальнях. Истоки музыкального строя: астрономия, время, число.
(Продолжение Истории о молотках и наковальнях)
Куда ведёт п о и с к?
Туда же, куда и тайна.
Прекрасная Лимма не принесла успокоения: « всё совершено, всё завершено». Наоборот, лишь раздразнила новыми обещаниями звуков неведомых, ещё не открытых, затаившихся в пространствах интервалов. Увлекла. Пифагора увлекла. А вслед – и Платона, и Боэция (того самого, что на фреске Рафаэля заглядывает в тайную книгу Пифагора через тысячу лет).
Что же пытался высмотреть Боэций в книге Пифагора? Ответ на какой вопрос он искал в этой книге? Боэций ведь был теоретиком музыки! В своей книге «Основы музыки» он написал загадочную фразу, которая стала головоломкой для многих учёных на много столетий вперёд. И фраза эта имела отношение к пифагоровым консонансам и свидетельствовала о том, что с этими консонансами дело обстояло далеко не так просто, как кажется вначале.
Вот что написал Боэций: «…quo sex toni superant diapason consonantia».
(Евгений Герцман, «Античное музыкальное мышление»,1986г.)
То есть, оказывается, что 6 тонов п р е в о с х о д я т диапазон консонансов, иначе – октаву. И превосходят на КОММУ (ещё одна красавица! Мало нам ЛИММЫ!).
Точное значение слова «комма» неизвестно. Известно только, что греки называли коммой что-то очень маленькое. Можно даже сказать «конечно маленькое», потому что у вокалистов, например, она означает конец звучания и время брать дыхание.
МИКРОИНТЕРВАЛ. Самый маленький интервал.
И эта крошка-комма перепрыгивала октаву?
Но если ознакомиться с принятой в наше время гипотезой пифагорова строя, то коммой там называют «увеличенную септиму БЕЗ октавы».
Кусочек таблицы пифагорова строя:

Рис. и пометки автора.
То эта комма «перепрыгивает», то «недопрыгивает»… Всю красивую картину консонансов ставит под вопрос. Из-за неё пифагоров строй стали считать незамкнутым – не кольцом, а спиралью.
А фраза Боэция как-то невольно подводит к мысли, что консонансы могли слегка фальшивить! На эту самую комму ( примерно на ¼ часть лиммы, то есть ¼ часть полутона, – так иногда представляют величину коммы).
Ещё эту комму пытаются рассчитывать так:
(3/2)¹² : (2/1)¹ = 531441/524288 ≈ 1,014
Но как бы её ни рассчитывали, просто не верится, что Пифагор мог допустить, чтобы лира Орфея или самого Аполлона звучала с фальшью!
…Платон обращал внимание на важность для Пифагора одной дроби: 73/72.
(73/72 = 1,0138888… ≈ 0,014)
Если ты был внимателен, когда рассматривал нашу ленту частот, которая привела к консонансам, ты не мог не заметить, что частоты интервалов пришли к согласию на отметке шкалы 72.
Вот в этом месте начинается самая захватывающая часть «детектива про комму»!
Что для Пифагора могла значить дробь 73/72?
Кажется, пришло время вспомнить нечто очень-очень-очень важное из жизни этого великого учёного-мыслителя. Кто он? – Он математик, философ и к о с м о л о г! Человек, обладавший глубоким знанием астрономии. В Греции, в свои юные годы, он получил эти знания из трудов тоже великого греческого мыслителя и астронома – Анаксимандра. «Научная экспедиция» в Египет длиною в два десятка лет отшлифовала эти знания и приблизила Пифагора к их истоку. Десяток лет в Вавилоне ввели его пытливый ум в соприкосновение с древней цивилизацией шумеров – «авторов» первых уравнений, первого земного календаря, 360˚ окружности, 3600 секунд времени, первой геометрии (с пентагоном и пентаграммой) и множества изобретений, включая арфу.
Похоже, шумеры были необычайно умны и невероятно любознательны. Сияющий сквозь тысячелетия огонь их Мысли был разжигаем вопросом: Что есть этот мир, в который они явились жить? Земляне искали ответа не только на Земле. О самóй Земле они вопрошали величественное, поражавшее красотой и волшебным сиянием светил Небо – космос, Вселенную. Ритмы Солнца, Луны и звёзд сплетались с ритмами их жизни.
Солнце, проплывая по волнам восходов и закатов, возвращалось к началу своего странствия среди звёзд примерно каждые 365 дней ( 365 волн/импульсов/доминант восходов-закатов – суток).
Луна плыла по волнам новолуний-полнолуний, возвращаясь к началу своего пути среди звёзд примерно каждые 355 ночей (суток).
А Земля кружилась посреди танца-кружения этих светил, между их притяжением, словно оказываясь в центре симметрии действия их могучих сил (Солнце – огромное и мощное, но очень далеко; Луна – маленькая в сравнении с Солнцем, но очень близко; силы уравновешивались).
В результате путь Земли между этими главными светилами казался замкнутым кольцом: согласие, созвучие движений всей этой космической триады (консонанс!) внутри сферы звёзд (четвёртый компонент) – всегда в одно и то же в р е м я; конец совпадал с началом, и всё повторялось из года в год.
Земля – посредине. Посредница. «Среднее арифметическое»: (365+355):2=360. 360 собственных «шагов» Земли в космических небесах, «шагов»-дуг по окружности её собственного движения-вращения.
360 г р а д у с о в.
(Градус – лат. gradus – «шаг», «ступень», «степень», «мера»).
Веками позднее египтяне эту мысль о космических ритмах жизни запечатлели в мифе о Времени.
Египетский миф о Времени.
Богиня справедливости Маат разделила год на времена:
Время разлива (Нила),
Время всходов,
Время урожая.
Все три времени года она поделила на месяцы – по четыре в каждом, и в каждом месяце – по 30 суток. А каждые сутки поделила поровну между Солнцем и Луной. Солнечный год был равен лунному: по 12 месяцев, 360 дней.
Хранительницей установленного порядка Маат назначила Луну. Но Луна не справилась со своей миссией, так как поневоле оказалась в центре ссоры между владыкой Вселенной – Великим Ра и своенравной богиней неба Нут.
Нут желала почитания, славы и могущества – не меньшего, чем у Ра.
Бог Вселенной разгневался и решил наказать тщеславную богиню неба.
«Я предаю проклятию все 360 дней года. Ни в один из этих дней ты не сможешь рожать детей и навсегда останешься бездетной!» – прогремел Ра.
Весь мир замер в страхе: что же будет?
Спасти ситуацию мог только бог мудрости (а также знаний и письменности) – Тот. Тот самый Тот, который всегда утверждал, что настоящая сила – ум.
Превратившись в ибиса, Тот полетел к хранительнице Времени Луне, удалившейся в пустыню и пребывавшей в великой печали.
Луна обрадовалась визиту дружелюбного гостя. Она желала, чтобы мгновения приятного общения с ним всё длились и длились. Не зная, чем удержать его, она вдруг предложила сыграть в шашки.
– А на что мы будем играть? – спросил Тот.
– У меня ничего нет, кроме света, которым я освещаю небо по ночам, – смутилась Луна.
– Будем играть на свет, – согласился Тот. – Не на весь, конечно. На часть.
В лунном году 360 дней. Возьми от каждого дня маленькую-маленькую часть, затем сложи эти части вместе – они и будут ставкой.
– Это невозможно, – огорчилась Луна. – Я хранительница Времени, я не могу отдать ни одного дня из лунного года.
– Не надо целого дня, – улыбнулся Тот. – Убавь от каждого дня всего по нескольку минут. 24/72 = 1/3 часа = 20 минут…
– Я убавлю от каждого дня маленький кусочек – всего 1/72 его часть, если ты, Тот, выиграешь. Даже никто не заметит, что лунные сутки стали короче, – согласилась Луна.
Тот кивнул, и игра началась.
…Тот выиграл.
Убавив от каждого дня всего несколько минут, Луна, как оказалось, получила значительный проигрыш. Когда Тот сложил эти минуты, вышло целых 5 суток! Отныне в лунном году осталось 355 дней.
А выигранные 5 дней Тот прибавил к солнечному году, в результате чего в солнечном году стало 365 дней.
В чём была хитрость Тота? – Выигранные им у Луны 5 дней не были преданы проклятию Ра! Ведь Ра проклял 360 дней, а не 365.
И выигранные дни Тот посвятил самому Ра. – Не станет же Владыка проклинать дни, посвящённые ему самому.
А Нут в эти 5 дней в конце года родила пятерых детей: Осириса, Гора Бехдетского, Сета, Исиду и Нефтиду, – тоже богов.
(И.В. Рак. Мифы и сказки древнего Египта.)
/Пересказ автора/
Эту самую 1/72 часть можно получить, если разделить окружность в 360˚ на 5 частей: по 72˚ каждая часть. И 1/72 часть каждой пятой части окружности будет равна 1˚. В пересчёте на дни 1˚ = 1 день. 5˚= 5дням.
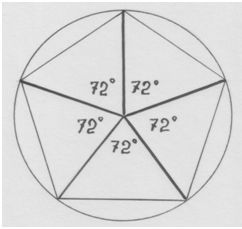
Рис. автора.
Лунный год будет выглядеть разомкнутым кольцом, а солнечный год – намёком на спираль. При этом получается, будто в каждой пятой части пятиугольника должен бы «набегать» один лишний градус – 73-й. А «по-лунному» – в каждой части 71 градус.
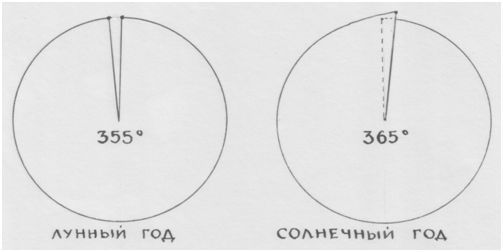
Рис. автора.
Замечательно то, что в ЦЕЛОМ и в каждой пятой части этого ЦЕЛОГО отношения остаются одинаковыми:
365/360 = 1, 0138888… 73/72 = 1, 0138888…
360/355 = 1, 0140845… 72/71 = 1, 0140845…
То есть, в данном случае в ЧАСТИ отражается ЦЕЛОЕ настолько полно, что даже можно поставить знак равенства.
Какие чудесные перспективы сулило это обстоятельство для Мысли Пифагора!
Звуковые консонансы – той же природы, что и космические! Вот она, пифагорова «музыка сфер»! Сферы небесных тел (Солнца, Земли, Луны, «неподвижных звёзд») в своём гармоничном согласии/созвучии подобны музыке! А музыка – рождена космосом, Вселенной! Всё – единый узел.
«10» – священное число! (Земля между Солнцем и Луной внутри звёздной сферы.)
И в самом деле, это ведь число двойного узла: правого и левого. Их совмещение рождает Пентаграмму – само совершенство Золотого сечения (хотя Пифагор не употреблял этого термина, как ты знаешь; но он постиг саму с у т ь этого явления, пронизывающего великое во Вселенной и малое на Земле). Это – взаимодействие квинт, прародительниц музыкального строя (квинт и их перевёртышей-кварт).
Да, всего лишь разница-разность между солнечным и лунным годом на Земле (10 дней – 10 градусов) и – поразительное совпадение звуковых консонансов в «пункте 72» плюс-минус крошка-комма.
«10» для Пифагора – число, к тому же, особое ещё и потому, что т р е у г о л ь н о е. Странно?
Если в д у м а т ь с я – то не странно.
Равносторонний треугольник знаменует собою идею совершенства-равенства: равенства сторон-отрезков и углов. Он подобен явлению «градуса» – меры, которой измеряют и углы, и дуги (углы и отрезки окружности).
В равносторонний треугольник вписывается само число «10» в виде точек-«узелков», скрепляющих внутренние подобные малые треугольники:
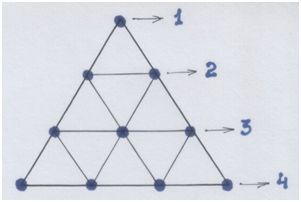
Рис. автора.
А теперь давай ещё разочек взглянём на уже известную нам таблицу гармоник, на ту её часть, где представлены совершенные консонансы в виде волн, бегущих туда-обратно:
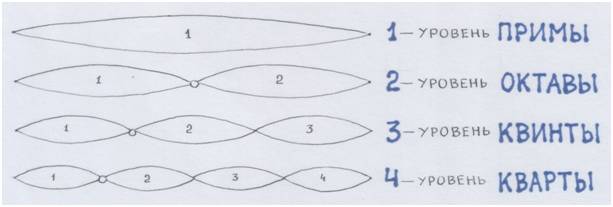
Рис. автора.
Совместим геометрический и волновой образы:
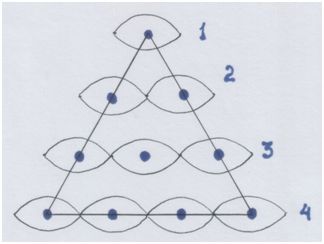
Рис. автора.
Попробуем совместить так, чтобы узлы совпадали. (У бегущих туда-обратно звуковых волн есть у з л ы и так называемые п у ч н о с т и. Об этом ты можешь узнать из книги проф. А.Г.Белявского «Теория звука в приложении к музыке»). Так нам треугольник покажет именно частоты или длины волн интервалов-консонансов в виде отношений/пропорций/дробей.
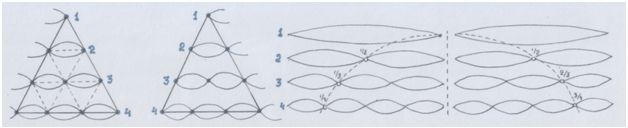
Рис. автора.
Музыкальный (и космический, конечно же) треугольник!
Музыкальная «десятка»!
Особенность всех чисел, принимающих участие в этой «магии» такова, что при сложении они и образуют «десятку»: 1+2+3+4 = 10
О, как непросто всё было у Пифагора!
Всё связано со всем.
А как же Пифагор поступил с КОММОЙ?
Комма своим явлением словно намекала на солнечное время на Земле (спираль солнечного года). Согласно Боэцию, она п р е в ы ш а л а консонанс диапазона-октавы («перехлёстывала через край»). Как солнечное время на Земле «перехлёстывает» кольцо в 360˚ на 5˚ (дней). На 1/72.
(Вот ещё раз: Звук и Время на Земле – одной природы, – космической!)
Те, кто думают, что Пифагор остановился, преткнулся о тот факт, что реальный звук словно не желает строго подчиняться консонансу (торопится вслед за Солнцем), они говорят, что пифагоров строй подобен спирали.
Но давай вглядимся повнимательнее в измерительный прибор Пифагора – монохорд: ящик. На ящике – шкала с делениями. Струна. Один конец струны закреплён жёстко колком, похожим на гвоздь. А другой конец струны свисает свободно. Он перекинут через колёсико-блок, и к нему подвешен груз. Ещё есть передвижная перекладина ( её называют «кобылкой», – наверное, потому что бегает туда-сюда) для изменения пропорций струны – чтобы получать различные интервалы-звуки.
Но нас интересует свободный конец струны. Для чего так?
Воспитывать КОММУ! Сдерживать её слишком солнечный темперамент. Приучать её к к о н с о н а н с у.
Пифагор был тем ещё Тотом! Только поступил он противоположно, и благодаря этому Луна получила возможность отыграться – вернуть свою 1/72 долю. Как?
Если частота звука слегка зашкаливает, то есть чуть выше, чем необходимо для консонанса, эту частоту можно изменить: понизить, уменьшить, – изменив натяжение струны, чуть ослабив его. Струна станет толще, «массивнее», «ленивее», будет колебаться менее активно. И напряжение звуковой волны уменьшится, и звук понизится в тоне. И комма вернётся в рамки диапазона. Кольцо замкнётся.
Для этого придётся вернуть 1/72 долю шкалы консонансов ( на нашей ленте частот) Луне. 73/72-х станут 72/72.
Как мог действовать Пифагор?
Сама проблема с коммой, по-видимому, возникла, когда пришлось приводить к консонансу звучание нескольких струн, изначально настроенных в соответствии с расчётами интервалов. Для этой цели служил другой прибор: полихорд (греч. polys – «многий», множество, horda – струна).
На этом приборе мы видим четыре струны для основных консонансов: примы, октавы, квинты, кварты.
Примой может стать любой тон-звук. От него и будут выстраиваться все остальные соотношения звуков. Разница в комму проявит себя на октавной струне (73/72= 1,0138888…). Она натянута в два раза сильнее струны примы (если жильная струна), или в два раза тоньше (если металлическая). Её натяжение нужно уменьшить на 1/72 (0,0138888….) и ещё совсем чуть-чуть. Об этом «чуть-чуть», может быть, ещё поговорим, если не устанем.
То есть:
Идеальная шкала консонансов по расчёту должна быть 72/72. Но при этом мы слышим звук на 1/72 выше расчетного, – как если бы шкала была 73/72. Чтобы услышать консонанс 72/72, нам нужно спуститься до отметки 71 (ослабить натяжение струны) – «по Луне». Тогда мы опять услышим звук на 1/72 выше, над отметкой 71,– т.е. 72/72.
Струна квинты (если жильная) натянута в полтора раза сильнее струны примы ( как если бы мы растянули 72 деления на длину 108; 72х1,5=108), или толщина её (если струна металлическая) = 2/3 толщины струны примы.
Что мы услышим? – Мы услышим звук тоже примерно на 1/72 выше нужного, т.е. не 108/72, а 109/72. Нам нужно ослабить натяжение струны до отметки 107 («по Луне»), и ещё чуть-чуть. Мы услышим то, что нужно: 0,0138888…х 108= 1,499…– «чуть-чуть».
Аналогично – со струной кварты.
Струна кварты (если жильная) натянута в 4/3 раза (примерно в 1,33333…. раза) сильнее струны примы (как если бы мы растянули 72 деления на на почти 96: 1,333333…х 72 = 95,999999…), или толщина струны (если струна металлическая) = ¾ струны примы.
Что мы услышим? – Мы услышим звук также примерно на 1/72 выше нужного, т.е. не 96/72, а 97/72. Нам нужно ослабить натяжение струны «по Луне», чтобы мы услышали необходимую высоту звука: 95/72 – «чуть-чуть».
Так можно поступать со струнами и для других интервальных звуков. На полихорде можно разместить и 6, и 7 струн для этих целей, – смоделировав таким образом лиру.
Странно ведёт себя звук. Мы слышим его «по Солнцу», а струны, чтобы получить консонансы, нужно настраивать «по Луне».
И здесь тоже не всё так просто, как в египетском мифе о Времени. Ведь солнечный год чуть больше 365 дней, за 4 года набегает своя «комма» примерно в одни сутки. Да и лунный год – не ровно 355 дней. Мы округляем, чтобы увидеть главные пропорции, увидеть структуру. Мы привыкли всё сводить к завершённости, к уравнениям. А движение существует благодаря неравенствам – пусть небольшим, с разницей в «чуть-чуть», но неравенствам.
Звук, как и Время, происходит из движения. Сами волны – это движение. Движение подразумевает какое-то неравенство. И конечно же, консонансы не могут быть идеальными. И наш слух готов мириться с небольшими неравенствами, которые держатся на «чуть-чуть». Мы их как будто не слышим – «округляем», как иррациональные числа мы склонны округлять.
Кстати, если ты когда-нибудь всё-таки заглянёшь в книгу А.Г.Белявского «Теория звука в приложении к музыке», ты узнаешь из рекомендаций настройщикам фортепиано, что чистые интервалы при настройке необходимо понижать – иначе консонансов не получится, настройка инструмента потерпит крах.
Пифагор об этом узнал из правил поведения космических объектов и обнаружил эти же правила в поведении звуков.
И Генрих Рудольф Герц, физик 19 века, «изобретатель» герца – единицы измерения частоты периодических процессов, в том числе волн, похоже, не противоречил Пифагору, соединившему космос, время, звук. Герц служит также единицей измерения времени.
Только в отношении звуковых волн Герц уточнил пифагорово «чуть-чуть». Например, интервал квинта определяется отношением частот не 1,5 или 1,499…(в переводе на десятичные дроби), а 1,498…

