The Canterbury Puzzles, and Other Curious Problems

88.—The Eccentric Market-woman

Mrs. Covey, who keeps a little poultry farm in Surrey, is one of the most eccentric women I ever met. Her manner of doing business is always original, and sometimes quite weird and wonderful. She was once found explaining to a few of her choice friends how she had disposed of her day's eggs. She had evidently got the idea from an old puzzle with which we are all familiar; but as it is an improvement on it, I have no hesitation in presenting it to my readers. She related that she had that day taken a certain number of eggs to market. She sold half of them to one customer, and gave him half an egg over. She next sold a third of what she had left, and gave a third of an egg over. She then sold a fourth of the remainder, and gave a fourth of an egg over. Finally, she disposed of a fifth of the remainder, and gave a fifth of an egg over. Then what she had left she divided equally among thirteen of her friends. And, strange to say, she had not throughout all these transactions broken a single egg. Now, the puzzle is to find the smallest possible number of eggs that Mrs. Covey could have taken to market. Can you say how many?

89.—The Primrose Puzzle

Select the name of any flower that you think suitable, and that contains eight letters. Touch one of the primroses with your pencil and jump over one of the adjoining flowers to another, on which you mark the first letter of your word. Then touch another vacant flower, and again jump over one in another direction, and write down the second letter. Continue this (taking the letters in their proper order) until all the letters have been written down, and the original word can be correctly read round the garland. You must always touch an unoccupied flower, but the flower jumped over may be occupied or not. The name of a tree may also be selected. Only English words may be used.

90.—The Round Table

Seven friends, named Adams, Brooks, Cater, Dobson, Edwards, Fry, and Green, were spending fifteen days together at the seaside, and they had a round breakfast table at the hotel all to themselves. It was agreed that no man should ever sit down twice with the same two neighbours. As they can be seated, under these conditions, in just fifteen ways, the plan was quite practicable. But could the reader have prepared an arrangement for every sitting? The hotel proprietor was asked to draw up a scheme, but he miserably failed.

91.—The Five Tea Tins

Sometimes people will speak of mere counting as one of the simplest operations in the world; but on occasions, as I shall show, it is far from easy. Sometimes the labour can be diminished by the use of little artifices; sometimes it is practically impossible to make the required enumeration without having a very clear head indeed. An ordinary child, buying twelve postage stamps, will almost instinctively say, when he sees there are four along one side and three along the other, "Four times three are twelve;" while his tiny brother will count them all in rows, "1, 2, 3, 4," etc. If the child's mother has occasion to add up the numbers 1, 2, 3, up to 50, she will most probably make a long addition sum of the fifty numbers; while her husband, more used to arithmetical operations, will see at a glance that by joining the numbers at the extremes there are 25 pairs of 51; therefore, 25×51=1,275. But his smart son of twenty may go one better and say, "Why multiply by 25? Just add two 0's to the 51 and divide by 4, and there you are!"

A tea merchant has five tin tea boxes of cubical shape, which he keeps on his counter in a row, as shown in our illustration. Every box has a picture on each of its six sides, so there are thirty pictures in all; but one picture on No. 1 is repeated on No. 4, and two other pictures on No. 4 are repeated on No. 3. There are, therefore, only twenty-seven different pictures. The owner always keeps No. 1 at one end of the row, and never allows Nos. 3 and 5 to be put side by side.

The tradesman's customer, having obtained this information, thinks it a good puzzle to work out in how many ways the boxes may be arranged on the counter so that the order of the five pictures in front shall never be twice alike. He found the making of the count a tough little nut. Can you work out the answer without getting your brain into a tangle? Of course, two similar pictures may be in a row, as it is all a question of their order.

92.—The Four Porkers

The four pigs are so placed, each in a separate sty, that although every one of the thirty-six sties is in a straight line (either horizontally, vertically, or diagonally), with at least one of the pigs, yet no pig is in line with another. In how many different ways may the four pigs be placed to fulfil these conditions? If you turn this page round you get three more arrangements, and if you turn it round in front of a mirror you get four more. These are not to be counted as different arrangements.

93.—The Number Blocks

The children in the illustration have found that a large number of very interesting and instructive puzzles may be made out of number blocks; that is, blocks bearing the ten digits or Arabic figures—1, 2, 3, 4, 5, 6, 7, 8, 9, and 0. The particular puzzle that they have been amusing themselves with is to divide the blocks into two groups of five, and then so arrange them in the form of two multiplication sums that one product shall be the same as the other. The number of possible solutions is very considerable, but they have hit on that arrangement that gives the smallest possible product. Thus, 3,485 multiplied by 2 is 6,970, and 6,970 multiplied by 1 is the same. You will find it quite impossible to get any smaller result.

Now, my puzzle is to find the largest possible result. Divide the blocks into any two groups of five that you like, and arrange them to form two multiplication sums that shall produce the same product and the largest amount possible. That is all, and yet it is a nut that requires some cracking. Of course, fractions are not allowed, nor any tricks whatever. The puzzle is quite interesting enough in the simple form in which I have given it. Perhaps it should be added that the multipliers may contain two figures.

94.—Foxes and Geese

Here is a little puzzle of the moving counters class that my readers will probably find entertaining. Make a diagram of any convenient size similar to that shown in our illustration, and provide six counters—three marked to represent foxes and three to represent geese. Place the geese on the discs 1, 2, and 3, and the foxes on the discs numbered 10, 11, and 12

Now the puzzle is this. By moving one at a time, fox and goose alternately, along a straight line from one disc to the next one, try to get the foxes on 1, 2, and 3, and the geese on 10, 11, and 12—that is, make them exchange places—in the fewest possible moves.

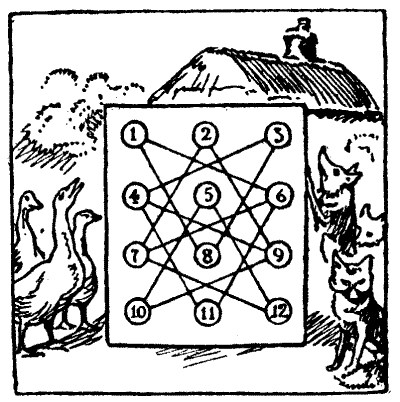
But you must be careful never to let a fox and goose get within reach of each other, or there will be trouble. This rule, you will find, prevents you moving the fox from 11 on the first move, as on either 4 or 6 he would be within reach of a goose. It also prevents your moving a fox from 10 to 9, or from 12 to 7. If you play 10 to 5, then your next move may be 2 to 9 with a goose, which you could not have played if the fox had not previously gone from 10. It is perhaps unnecessary to say that only one fox or one goose can be on a disc at the same time. Now, what is the smallest number of moves necessary to make the foxes and geese change places?

95.—Robinson Crusoe's Table

Here is a curious extract from Robinson Crusoe's diary. It is not to be found in the modern editions of the Adventures, and is omitted in the old. This has always seemed to me to be a pity.

"The third day in the morning, the wind having abated during the night, I went down to the shore hoping to find a typewriter and other useful things washed up from the wreck of the ship; but all that fell in my way was a piece of timber with many holes in it. My man Friday had many times said that we stood sadly in need of a square table for our afternoon tea, and I bethought me how this piece of wood might be used for that purpose. And since during the long time that Friday had now been with me I was not wanting to lay a foundation of useful knowledge in his mind, I told him that it was my wish to make the table from the timber I had found, without there being any holes in the top thereof.

"Friday was sadly put to it to say how this might be, more especially as I said it should consist of no more than two pieces joined together; but I taught him how it could be done in such a way that the table might be as large as was possible, though, to be sure, I was amused when he said, 'My nation do much better: they stop up holes, so pieces sugars not fall through.'"

Now, the illustration gives the exact proportion of the piece of wood with the positions of the fifteen holes. How did Robinson Crusoe make the largest possible square table-top in two pieces, so that it should not have any holes in it?

96.—The Fifteen Orchards

In the county of Devon, where the cider comes from, fifteen of the inhabitants of a village are imbued with an excellent spirit of friendly rivalry, and a few years ago they decided to settle by actual experiment a little difference of opinion as to the cultivation of apple trees. Some said they want plenty of light and air, while others stoutly maintained that they ought to be planted pretty closely, in order that they might get shade and protection from cold winds. So they agreed to plant a lot of young trees, a different number in each orchard, in order to compare results.

One man had a single tree in his field, another had two trees, another had three trees, another had four trees, another five, and so on, the last man having as many as fifteen trees in his little orchard. Last year a very curious result was found to have come about. Each of the fifteen individuals discovered that every tree in his own orchard bore exactly the same number of apples. But, what was stranger still, on comparing notes they found that the total gathered in every allotment was almost the same. In fact, if the man with eleven trees had given one apple to the man who had seven trees, and the man with fourteen trees had given three each to the men with nine and thirteen trees, they would all have had exactly the same.

Now, the puzzle is to discover how many apples each would have had (the same in every case) if that little distribution had been carried out. It is quite easy if you set to work in the right way.

97.—The Perplexed Plumber

When I paid a visit to Peckham recently I found everybody asking, "What has happened to Sam Solders, the plumber?" He seemed to be in a bad way, and his wife was seriously anxious about the state of his mind. As he had fitted up a hot-water apparatus for me some years ago which did not lead to an explosion for at least three months (and then only damaged the complexion of one of the cook's followers), I had considerable regard for him.

"There he is," said Mrs. Solders, when I called to inquire. "That's how he's been for three weeks. He hardly eats anything, and takes no rest, whilst his business is so neglected that I don't know what is going to happen to me and the five children. All day long—and night too—there he is, figuring and figuring, and tearing his hair like a mad thing. It's worrying me into an early grave."

I persuaded Mrs. Solders to explain matters to me. It seems that he had received an order from a customer to make two rectangular zinc cisterns, one with a top and the other without a top. Each was to hold exactly 1,000 cubic feet of water when filled to the brim. The price was to be a certain amount per cistern, including cost of labour. Now Mr. Solders is a thrifty man, so he naturally desired to make the two cisterns of such dimensions that the smallest possible quantity of metal should be required. This was the little question that was so worrying him.

Can my ingenious readers find the dimensions of the most economical cistern with a top, and also the exact proportions of such a cistern without a top, each to hold 1,000 cubic feet of water? By "economical" is meant the method that requires the smallest possible quantity of metal. No margin need be allowed for what ladies would call "turnings." I shall show how I helped Mr. Solders out of his dilemma. He says: "That little wrinkle you gave me would be useful to others in my trade."

98.—The Nelson Column

During a Nelson celebration I was standing in Trafalgar Square with a friend of puzzling proclivities. He had for some time been gazing at the column in an abstracted way, and seemed quite unconscious of the casual remarks that I addressed to him.

"What are you dreaming about?" I said at last.

"Two feet–" he murmured.

"Somebody's Trilbys?" I inquired.

"Five times round–"

"Two feet, five times round! What on earth are you saying?"

"Wait a minute," he said, beginning to figure something out on the back of an envelope. I now detected that he was in the throes of producing a new problem of some sort, for I well knew his methods of working at these things.

"Here you are!" he suddenly exclaimed. "That's it! A very interesting little puzzle. The height of the shaft of the Nelson column being 200 feet and its circumference 16 feet 8 inches, it is wreathed in a spiral garland which passes round it exactly five times. What is the length of the garland? It looks rather difficult, but is really remarkably easy."

He was right. The puzzle is quite easy if properly attacked. Of course the height and circumference are not correct, but chosen for the purposes of the puzzle. The artist has also intentionally drawn the cylindrical shaft of the column of equal circumference throughout. If it were tapering, the puzzle would be less easy.

99.—The Two Errand Boys

A country baker sent off his boy with a message to the butcher in the next village, and at the same time the butcher sent his boy to the baker. One ran faster than the other, and they were seen to pass at a spot 720 yards from the baker's shop. Each stopped ten minutes at his destination and then started on the return journey, when it was found that they passed each other at a spot 400 yards from the butcher's. How far apart are the two tradesmen's shops? Of course each boy went at a uniform pace throughout.

100.—On the Ramsgate Sands

Thirteen youngsters were seen dancing in a ring on the Ramsgate sands. Apparently they were playing "Round the Mulberry Bush." The puzzle is this. How many rings may they form without any child ever taking twice the hand of any other child—right hand or left? That is, no child may ever have a second time the same neighbour.

101.—The Three Motor-Cars

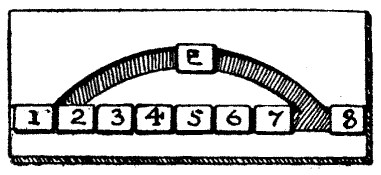
Pope has told us that all chance is but "direction which thou canst not see," and certainly we all occasionally come across remarkable coincidences—little things against the probability of the occurrence of which the odds are immense—that fill us with bewilderment. One of the three motor men in the illustration has just happened on one of these queer coincidences. He is pointing out to his two friends that the three numbers on their cars contain all the figures 1 to 9 and 0, and, what is more remarkable, that if the numbers on the first and second cars are multiplied together they will make the number on the third car. That is, 78, 345, and 26,910 contain all the ten figures, and 78 multiplied by 345 makes 26,910. Now, the reader will be able to find many similar sets of numbers of two, three, and five figures respectively that have the same peculiarity. But there is one set, and one only, in which the numbers have this additional peculiarity—that the second number is a multiple of the first. In other words, if 345 could be divided by 78 without a remainder, the numbers on the cars would themselves fulfil this extra condition. What are the three numbers that we want? Remember that they must have two, three, and five figures respectively.

102.—A Reversible Magic Square

Can you construct a square of sixteen different numbers so that it shall be magic (that is, adding up alike in the four rows, four columns, and two diagonals), whether you turn the diagram upside down or not? You must not use a 3, 4, or 5, as these figures will not reverse; but a 6 may become a 9 when reversed, a 9 a 6, a 7 a 2, and a 2 a 7. The 1, 8, and 0 will read the same both ways. Remember that the constant must not be changed by the reversal.

103.—The Tube Railway

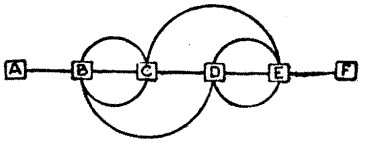
The above diagram is the plan of an underground railway. The fare is uniform for any distance, so long as you do not go twice along any portion of the line during the same journey. Now a certain passenger, with plenty of time on his hands, goes daily from A to F. How many different routes are there from which he may select? For example, he can take the short direct route, A, B, C, D, E, F, in a straight line; or he can go one of the long routes, such as A, B, D, C, B, C, E, D, E, F. It will be noted that he has optional lines between certain stations, and his selections of these lead to variations of the complete route. Many readers will find it a very perplexing little problem, though its conditions are so simple.

104.—The Skipper and the Sea-Serpent

Mr. Simon Softleigh had spent most of his life between Tooting Bec and Fenchurch Street. His knowledge of the sea was therefore very limited. So, as he was taking a holiday on the south coast, he thought this was a splendid opportunity for picking up a little useful information. He therefore proceeded to "draw" the natives.

"I suppose," said Mr. Softleigh one morning to a jovial, weather-beaten skipper, "you have seen many wonderful sights on the rolling seas?"

"Bless you, sir, yes," said the skipper. "P'raps you've never seen a vanilla iceberg, or a mermaid a-hanging out her things to dry on the equatorial line, or the blue-winged shark what flies through the air in pursuit of his prey, or the sea-sarpint–"

"Have you really seen a sea-serpent? I thought it was uncertain whether they existed."

"Uncertin! You wouldn't say there was anything uncertin about a sea-sarpint if once you'd seen one. The first as I seed was when I was skipper of the Saucy Sally. We was a-coming round Cape Horn with a cargo of shrimps from the Pacific Islands when I looks over the port side and sees a tremenjus monster like a snake, with its 'ead out of the water and its eyes flashing fire, a-bearing down on our ship. So I shouts to the bo'sun to let down the boat, while I runs below and fetches my sword—the same what I used when I killed King Chokee, the cannibal chief as eat our cabin-boy—and we pulls straight into the track of that there sea-sarpint. Well, to make a long story short, when we come alongside o' the beast I just let drive at him with that sword o' mine, and before you could say 'Tom Bowling' I cut him into three pieces, all of exactually the same length, and afterwards we hauled 'em aboard the Saucy Sally. What did I do with 'em? Well, I sold 'em to a feller in Rio Janeiro. And what do you suppose he done with 'em? He used 'em to make tyres for his motor-car—takes a lot to puncture a sea-sarpint's skin."

"What was the length of the creature?" asked Simon.

"Well, each piece was equal in length to three-quarters the length of a piece added to three-quarters of a cable. There's a little puzzle for you to work out, young gentleman. How many cables long must that there sea-sarpint 'ave been?"

Now, it is not at all to the discredit of Mr. Simon Softleigh that he never succeeded in working out the correct answer to that little puzzle, for it may confidently be said that out of a thousand readers who attempt the solution not one will get it exactly right.

105.—The Dorcas Society

At the close of four and a half months' hard work, the ladies of a certain Dorcas Society were so delighted with the completion of a beautiful silk patchwork quilt for the dear curate that everybody kissed everybody else, except, of course, the bashful young man himself, who only kissed his sisters, whom he had called for, to escort home. There were just a gross of osculations altogether. How much longer would the ladies have taken over their needlework task if the sisters of the curate referred to had played lawn tennis instead of attending the meetings? Of course we must assume that the ladies attended regularly, and I am sure that they all worked equally well. A mutual kiss here counts as two osculations.

106.—The Adventurous Snail

A simple version of the puzzle of the climbing snail is familiar to everybody. We were all taught it in the nursery, and it was apparently intended to inculcate the simple moral that we should never slip if we can help it. This is the popular story. A snail crawls up a pole 12 feet high, ascending 3 feet every day and slipping back 2 feet every night. How long does it take to get to the top? Of course, we are expected to say the answer is twelve days, because the creature makes an actual advance of 1 foot in every twenty-four hours. But the modern infant in arms is not taken in in this way. He says, correctly enough, that at the end of the ninth day the snail is 3 feet from the top, and therefore reaches the summit of its ambition on the tenth day, for it would cease to slip when it had got to the top.

Let us, however, consider the original story. Once upon a time two philosophers were walking in their garden, when one of them espied a highly respectable member of the Helix Aspersa family, a pioneer in mountaineering, in the act of making the perilous ascent of a wall 20 feet high. Judging by the trail, the gentleman calculated that the snail ascended 3 feet each day, sleeping and slipping back 2 feet every night.

"Pray tell me," said the philosopher to his friend, who was in the same line of business, "how long will it take Sir Snail to climb to the top of the wall and descend the other side? The top of the wall, as you know, has a sharp edge, so that when he gets there he will instantly begin to descend, putting precisely the same exertion into his daily climbing down as he did in his climbing up, and sleeping and slipping at night as before."