The Canterbury Puzzles, and Other Curious Problems

73.—The Game of Kayles

Nearly all of our most popular games are of very ancient origin, though in many cases they have been considerably developed and improved. Kayles—derived from the French word quilles—was a great favourite in the fourteenth century, and was undoubtedly the parent of our modern game of ninepins. Kayle-pins were not confined in those days to any particular number, and they were generally made of a conical shape and set up in a straight row.

At first they were knocked down by a club that was thrown at them from a distance, which at once suggests the origin of the pastime of "shying for cocoanuts" that is to-day so popular on Bank Holidays on Hampstead Heath and elsewhere. Then the players introduced balls, as an improvement on the club.

In the illustration we get a picture of some of our fourteenth-century ancestors playing at kayle-pins in this manner.

Now, I will introduce to my readers a new game of parlour kayle-pins, that can be played across the table without any preparation whatever. You simply place in a straight row thirteen dominoes, chess-pawns, draughtsmen, counters, coins, or beans—anything will do—all close together, and then remove the second one as shown in the picture.

It is assumed that the ancient players had become so expert that they could always knock down any single kayle-pin, or any two kayle-pins that stood close together. They therefore altered the game, and it was agreed that the player who knocked down the last pin was the winner.

Therefore, in playing our table-game, all you have to do is to knock down with your fingers, or take away, any single kayle-pin or two adjoining kayle-pins, playing alternately until one of the two players makes the last capture, and so wins. I think it will be found a fascinating little game, and I will show the secret of winning.

Remember that the second kayle-pin must be removed before you begin to play, and that if you knock down two at once those two must be close together, because in the real game the ball could not do more than this.

74.—The Broken Chessboard

There is a story of Prince Henry, son of William the Conqueror, afterwards Henry I., that is so frequently recorded in the old chronicles that it is doubtless authentic. The following version of the incident is taken from Hayward's Life of William the Conqueror, published in 1613—

"Towards the end of his reigne he appointed his two sonnes Robert and Henry, with joynt authoritie, governours of Normandie; the one to suppresse either the insolence or levitie of the other. These went together to visit the French king lying at Constance: where, entertaining the time with varietie of disports, Henry played with Louis, then Daulphine of France, at chesse, and did win of him very much.

"Hereat Louis beganne to growe warme in words, and was therein little respected by Henry. The great impatience of the one and the small forbearance of the other did strike in the end such a heat between them that Louis threw the chessmen at Henry's face.

"Henry again stroke Louis with the chessboard, drew blood with the blowe, and had presently slain him upon the place had he not been stayed by his brother Robert.

"Hereupon they presently went to horse, and their spurres claimed so good haste as they recovered Pontoise, albeit they were sharply pursued by the French."

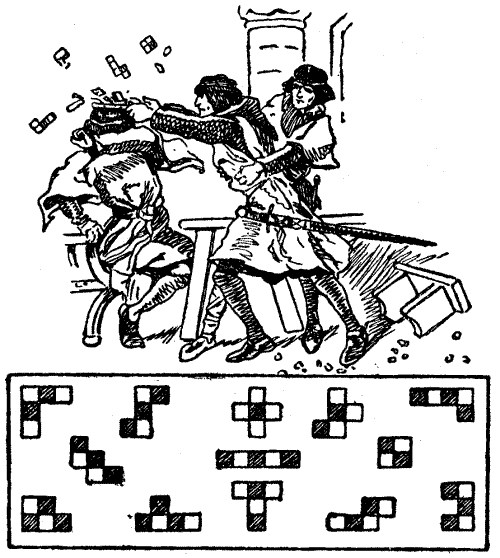
Now, tradition—on this point not trustworthy—says that the chessboard broke into the thirteen fragments shown in our illustration. It will be seen that there are twelve pieces, all different in shape, each containing five squares, and one little piece of four squares only.

We thus have all the sixty-four squares of the chess-board, and the puzzle is simply to cut them out and fit them together, so as to make a perfect board properly chequered. The pieces may be easily cut out of a sheet of "squared" paper, and, if mounted on cardboard, they will form a source of perpetual amusement in the home.

If you succeed in constructing the chessboard, but do not record the arrangement, you will find it just as puzzling the next time you feel disposed to attack it.

Prince Henry himself, with all his skill and learning, would have found it an amusing pastime.

75.—The Spider and the Fly

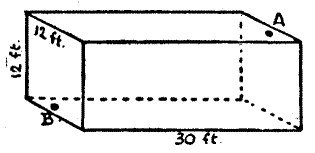
Inside a rectangular room, measuring 30 feet in length and 12 feet in width and height, a spider is at a point on the middle of one of the end walls, 1 foot from the ceiling, as at A; and a fly is on the opposite wall, 1 foot from the floor in the centre, as shown at B. What is the shortest distance that the spider must crawl in order to reach the fly, which remains stationary? Of course the spider never drops or uses its web, but crawls fairly.

76.—The Perplexed Cellarman

Here is a little puzzle culled from the traditions of an old monastery in the west of England. Abbot Francis, it seems, was a very worthy man; and his methods of equity extended to those little acts of charity for which he was noted for miles round.

The Abbot, moreover, had a fine taste in wines. On one occasion he sent for the cellarman, and complained that a particular bottling was not to his palate.

"Pray tell me, Brother John, how much of this wine thou didst bottle withal."

"A fair dozen in large bottles, my lord abbot, and the like in the small," replied the cellarman, "whereof five of each have been drunk in the refectory."

"So be it. There be three varlets waiting at the gate. Let the two dozen bottles be given unto them, both full and empty; and see that the dole be fairly made, so that no man receive more wine than another, nor any difference in bottles."

Poor John returned to his cellar, taking the three men with him, and then his task began to perplex him. Of full bottles he had seven large and seven small, and of empty bottles five large and five small, as shown in the illustration. How was he to make the required equitable division?

He divided the bottles into three groups in several ways that at first sight seemed to be quite fair, since two small bottles held just the same quantity of wine as one large one. But the large bottles themselves, when empty, were not worth two small ones.

Hence the abbot's order that each man must take away the same number of bottles of each size.

Finally, the cellarman had to consult one of the monks who was good at puzzles of this kind, and who showed him how the thing was done. Can you find out just how the distribution was made?

77.—Making a Flag

A good dissection puzzle in so few as two pieces is rather a rarity, so perhaps the reader will be interested in the following. The diagram represents a piece of bunting, and it is required to cut it into two pieces (without any waste) that will fit together and form a perfectly square flag, with the four roses symmetrically placed. This would be easy enough if it were not for the four roses, as we should merely have to cut from A to B, and insert the piece at the bottom of the flag. But we are not allowed to cut through any of the roses, and therein lies the difficulty of the puzzle. Of course we make no allowance for "turnings."

78.—Catching the Hogs

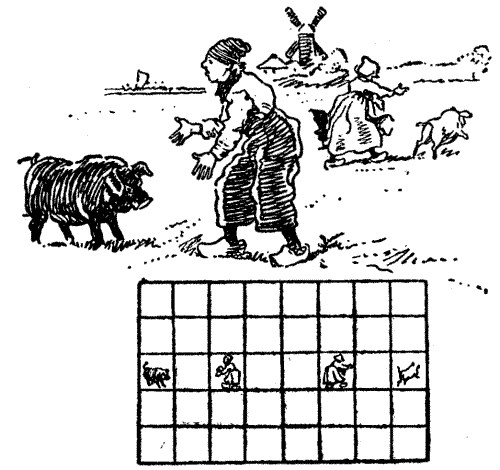
In the illustration Hendrick and Katrün are seen engaged in the exhilarating sport of attempting the capture of a couple of hogs.

Why did they fail?

Strange as it may seem, a complete answer is afforded in the little puzzle game that I will now explain.

Copy the simple diagram on a conveniently large sheet of cardboard or paper, and use four marked counters to represent the Dutchman, his wife, and the two hogs.

At the beginning of the game these must be placed on the squares on which they are shown. One player represents Hendrick and Katrün, and the other the hogs. The first player moves the Dutchman and his wife one square each in any direction (but not diagonally), and then the second player moves both pigs one square each (not diagonally); and so on, in turns, until Hendrick catches one hog and Katrün the other.

This you will find would be absurdly easy if the hogs moved first, but this is just what Dutch pigs will not do.

79.—The Thirty-one Game

This is a game that used to be (and may be to this day, for aught I know) a favourite means of swindling employed by card-sharpers at racecourses and in railway carriages.

As, on its own merits, however, the game is particularly interesting, I will make no apology for presenting it to my readers.

The cardsharper lays down the twenty-four cards shown in the illustration, and invites the innocent wayfarer to try his luck or skill by seeing which of them can first score thirty-one, or drive his opponent beyond, in the following manner:—

One player turns down a card, say a 2, and counts "two"; the second player turns down a card, say a 5, and, adding this to the score, counts "seven"; the first player turns down another card, say a 1, and counts "eight"; and so the play proceeds alternately until one of them scores the "thirty-one," and so wins.

Now, the question is, in order to win, should you turn down the first card, or courteously request your opponent to do so? And how should you conduct your play? The reader will perhaps say: "Oh, that is easy enough. You must play first, and turn down a 3; then, whatever your opponent does, he cannot stop your making ten, or stop your making seventeen, twenty-four, and the winning thirty-one. You have only to secure these numbers to win."

But this is just that little knowledge which is such a dangerous thing, and it places you in the hands of the sharper.

You play 3, and the sharper plays 4 and counts "seven"; you play 3 and count "ten"; the sharper turns down 3 and scores "thirteen"; you play 4 and count "seventeen"; the sharper plays a 4 and counts "twenty-one"; you play 3 and make your "twenty-four."

Now the sharper plays the last 4 and scores "twenty-eight." You look in vain for another 3 with which to win, for they are all turned down! So you are compelled either to let him make the "thirty-one" or to go yourself beyond, and so lose the game.

You thus see that your method of certainly winning breaks down utterly, by what may be called the "method of exhaustion." I will give the key to the game, showing how you may always win; but I will not here say whether you must play first or second: you may like to find it out for yourself.

80.—The Chinese Railways

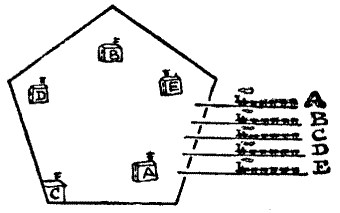
Our illustration shows the plan of a Chinese city protected by pentagonal fortifications. Five European Powers were scheming and clamouring for a concession to run a railway to the place; and at last one of the Emperor's more brilliant advisers said, "Let every one of them have a concession!" So the Celestial Government officials were kept busy arranging the details. The letters in the diagram show the different nationalities, and indicate not only just where each line must enter the city, but also where the station belonging to that line must be located. As it was agreed that the line of one company must never cross the line of another, the representatives of the various countries concerned were engaged so many weeks in trying to find a solution to the problem, that in the meantime a change in the Chinese Government was brought about, and the whole scheme fell through. Take your pencil and trace out the route for the line A to A, B to B, C to C, and so on, without ever allowing one line to cross another or pass through another company's station.

81.—The Eight Clowns

This illustration represents a troupe of clowns I once saw on the Continent. Each clown bore one of the numbers 1 to 9 on his body. After going through the usual tumbling, juggling, and other antics, they generally concluded with a few curious little numerical tricks, one of which was the rapid formation of a number of magic squares. It occurred to me that if clown No. 1 failed to appear (as happens in the illustration), this last item of their performance might not be so easy. The reader is asked to discover how these eight clowns may arrange themselves in the form of a square (one place being vacant), so that every one of the three columns, three rows, and each of the two diagonals shall add up the same. The vacant place may be at any part of the square, but it is No. 1 that must be absent.

82.—The Wizard's Arithmetic

Once upon a time a knight went to consult a certain famous wizard. The interview had to do with an affair of the heart; but after the man of magic had foretold the most favourable issues, and concocted a love-potion that was certain to help his visitor's cause, the conversation drifted on to occult subjects generally.

"And art thou learned also in the magic of numbers?" asked the knight. "Show me but one sample of thy wit in these matters."

The old wizard took five blocks bearing numbers, and placed them on a shelf, apparently at random, so that they stood in the order 41096, as shown in our illustration. He then took in his hands an 8 and a 3, and held them together to form the number 83.

"Sir Knight, tell me," said the wizard, "canst thou multiply one number into the other in thy mind?"

"Nay, of a truth," the good knight replied. "I should need to set out upon the task with pen and scrip."

"Yet mark ye how right easy a thing it is to a man learned in the lore of far Araby, who knoweth all the magic that is hid in the philosophy of numbers!"

The wizard simply placed the 3 next to the 4 on the shelf, and the 8 at the other end. It will be found that this gives the answer quite correctly—3410968. Very curious, is it not? How many other two-figure multipliers can you find that will produce the same effect? You may place just as many blocks as you like on the shelf, bearing any figures you choose.

83.—The Ribbon Problem

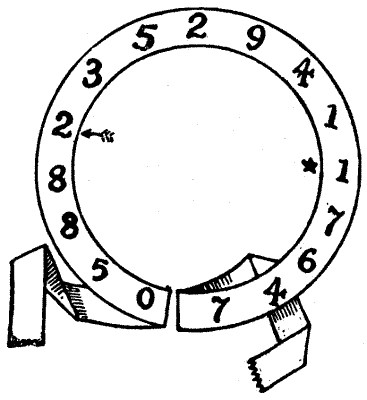
If we take the ribbon by the ends and pull it out straight, we have the number 0588235294117647. This number has the peculiarity that, if we multiply it by any one of the numbers, 2, 3, 4, 5, 6, 7, 8, or 9, we get exactly the same number in the circle, starting from a different place. For example, multiply by 4, and the product is 2352941176470588, which starts from the dart in the circle. So, if we multiply by 3, we get the same result starting from the star. Now, the puzzle is to place a different arrangement of figures on the ribbon that will produce similar results when so multiplied; only the 0 and the 7 appearing at the ends of the ribbon must not be removed.

84.—The Japanese Ladies and the Carpet

Three Japanese ladies possessed a square ancestral carpet of considerable intrinsic value, but treasured also as an interesting heirloom in the family. They decided to cut it up and make three square rugs of it, so that each should possess a share in her own house.

One lady suggested that the simplest way would be for her to take a smaller share than the other two, because then the carpet need not be cut into more than four pieces.

There are three easy ways of doing this, which I will leave the reader for the present the amusement of finding for himself, merely saying that if you suppose the carpet to be nine square feet, then one lady may take a piece two feet square whole, another a two feet square in two pieces, and the third a square foot whole.

But this generous offer would not for a moment be entertained by the other two sisters, who insisted that the square carpet should be so cut that each should get a square mat of exactly the same size.

Now, according to the best Western authorities, they would have found it necessary to cut the carpet into seven pieces; but a correspondent in Tokio assures me that the legend is that they did it in as few as six pieces, and he wants to know whether such a thing is possible.

Yes; it can be done.

Can you cut out the six pieces that will form three square mats of equal size?

85.—Captain Longbow and the Bears

That eminent and more or less veracious traveller Captain Longbow has a great grievance with the public. He claims that during a recent expedition in Arctic regions he actually reached the North Pole, but cannot induce anybody to believe him. Of course, the difficulty in such cases is to produce proof, but he avers that future travellers, when they succeed in accomplishing the same feat, will find evidence on the spot. He says that when he got there he saw a bear going round and round the top of the pole (which he declares is a pole), evidently perplexed by the peculiar fact that no matter in what direction he looked it was always due south. Captain Longbow put an end to the bear's meditations by shooting him, and afterwards impaling him, in the manner shown in the illustration, as the evidence for future travellers to which I have alluded.

When the Captain got one hundred miles south on his return journey he had a little experience that is somewhat puzzling. He was surprised one morning, on looking down from an elevation, to see no fewer than eleven bears in his immediate vicinity. But what astonished him more than anything else was the curious fact that they had so placed themselves that there were seven rows of bears, with four bears in every row. Whether or not this was the result of pure accident he cannot say, but such a thing might have happened. If the reader tries to make eleven dots on a sheet of paper so that there shall be seven rows of dots with four dots in every row, he will find some difficulty; but the captain's alleged grouping of the bears is quite possible. Can you discover how they were arranged?

86.—The English Tour

This puzzle has to do with railway routes, and in these days of much travelling should prove useful. The map of England shows twenty-four towns, connected by a system of railways. A resident at the town marked A at the top of the map proposes to visit every one of the towns once and only once, and to finish up his tour at Z. This would be easy enough if he were able to cut across country by road, as well as by rail, but he is not. How does he perform the feat? Take your pencil and, starting from A, pass from town to town, making a dot in the towns you have visited, and see if you can end at Z.

87.—The Chifu-Chemulpo Puzzle

Here is a puzzle that was once on sale in the London shops. It represents a military train—an engine and eight cars. The puzzle is to reverse the cars, so that they shall be in the order 8, 7, 6, 5, 4, 3, 2, 1, instead of 1, 2, 3, 4, 5, 6, 7, 8, with the engine left, as at first, on the side track. Do this in the fewest possible moves. Every time the engine or a car is moved from the main to the side track, or vice versa, it counts a move for each car or engine passed over one of the points. Moves along the main track are not counted. With 8 at the extremity, as shown, there is just room to pass 7 on to the side track, run 8 up to 6, and bring down 7 again; or you can put as many as five cars, or four and the engine, on the siding at the same time. The cars move without the aid of the engine. The purchaser is invited to "try to do it in 20 moves." How many do you require?