The Canterbury Puzzles, and Other Curious Problems

63.—The Cornish Cliff Mystery

Though the incident known in the Club as "The Cornish Cliff Mystery" has never been published, every one remembers the case with which it was connected—an embezzlement at Todd's Bank in Cornhill a few years ago. Lamson and Marsh, two of the firm's clerks, suddenly disappeared; and it was found that they had absconded with a very large sum of money. There was an exciting hunt for them by the police, who were so prompt in their action that it was impossible for the thieves to get out of the country. They were traced as far as Truro, and were known to be in hiding in Cornwall.

Just at this time it happened that Henry Melville and Fred Wilson were away together on a walking tour round the Cornish coast. Like most people, they were interested in the case; and one morning, while at breakfast at a little inn, they learnt that the absconding men had been tracked to that very neighbourhood, and that a strong cordon of police had been drawn round the district, making an escape very improbable. In fact, an inspector and a constable came into the inn to make some inquiries, and exchanged civilities with the two members of the Puzzle Club. A few references to some of the leading London detectives, and the production of a confidential letter Melville happened to have in his pocket from one of them, soon established complete confidence, and the inspector opened out.

He said that he had just been to examine a very important clue a quarter of a mile from there, and expressed the opinion that Messrs. Lamson and Marsh would never again be found alive. At the suggestion of Melville the four men walked along the road together.

"There is our stile in the distance," said the inspector. "This constable found beside it the pocket-book that I have shown you, containing the name of Marsh and some memoranda in his handwriting. It had evidently been dropped by accident. On looking over the stone stile he noticed the footprints of two men—which I have already proved from particulars previously supplied to the police to be those of the men we want—and I am sure you will agree that they point to only one possible conclusion."

Arrived at the spot, they left the hard road and got over the stile. The footprints of the two men were here very clearly impressed in the thin but soft soil, and they all took care not to trample on the tracks. They followed the prints closely, and found that they led straight to the edge of a cliff forming a sheer precipice, almost perpendicular, at the foot of which the sea, some two hundred feet below, was breaking among the boulders.

"Here, gentlemen, you see," said the inspector, "that the footprints lead straight to the edge of the cliff, where there is a good deal of trampling about, and there end. The soil has nowhere been disturbed for yards around, except by the footprints that you see. The conclusion is obvious."

"That, knowing they were unable to escape capture, they decided not to be taken alive, and threw themselves over the cliff?" asked Wilson.

"Exactly. Look to the right and the left, and you will find no footprints or other marks anywhere. Go round there to the left, and you will be satisfied that the most experienced mountaineer that ever lived could not make a descent, or even anywhere get over the edge of the cliff. There is no ledge or foothold within fifty feet."

"Utterly impossible," said Melville, after an inspection. "What do you propose to do?"

"I am going straight back to communicate the discovery to headquarters. We shall withdraw the cordon and search the coast for the dead bodies."

"Then you will make a fatal mistake," said Melville. "The men are alive and in hiding in the district. Just examine the prints again. Whose is the large foot?"

"That is Lamson's, and the small print is Marsh's. Lamson was a tall man, just over six feet, and Marsh was a little fellow."

"I thought as much," said Melville. "And yet you will find that Lamson takes a shorter stride than Marsh. Notice, also, the peculiarity that Marsh walks heavily on his heels, while Lamson treads more on his toes. Nothing remarkable in that? Perhaps not; but has it occurred to you that Lamson walked behind Marsh? Because you will find that he sometimes treads over Marsh's footsteps, though you will never find Marsh treading in the steps of the other."

"Do you suppose that the men walked backwards in their own footprints?" asked the inspector.

"No; that is impossible. No two men could walk backwards some two hundred yards in that way with such exactitude. You will not find a single place where they have missed the print by even an eighth of an inch. Quite impossible. Nor do I suppose that two men, hunted as they were, could have provided themselves with flying-machines, balloons, or even parachutes. They did not drop over the cliff."

Melville then explained how the men had got away. His account proved to be quite correct, for it will be remembered that they were caught, hiding under some straw in a barn, within two miles of the spot. How did they get away from the edge of the cliff?

64.—The Runaway Motor-Car

The little affair of the "Runaway Motor-car" is a good illustration of how a knowledge of some branch of puzzledom may be put to unexpected use. A member of the Club, whose name I have at the moment of writing forgotten, came in one night and said that a friend of his was bicycling in Surrey on the previous day, when a motor-car came from behind, round a corner, at a terrific speed, caught one of his wheels, and sent him flying in the road. He was badly knocked about, and fractured his left arm, while his machine was wrecked. The motor-car was not stopped, and he had been unable to trace it.

There were two witnesses to the accident, which was beyond question the fault of the driver of the car. An old woman, a Mrs. Wadey, saw the whole thing, and tried to take the number of the car. She was positive as to the letters, which need not be given, and was certain also that the first figure was a 1. The other figures she failed to read on account of the speed and dust.

The other witness was the village simpleton, who just escapes being an arithmetical genius, but is excessively stupid in everything else.

He is always working out sums in his head; and all he could say was that there were five figures in the number, and that he found that when he multiplied the first two figures by the last three they made the same figures, only in different order—just as 24 multiplied by 651 makes 15,624 (the same five figures), in which case the number of the car would have been 24,651; and he knew there was no 0 in the number.

"It will be easy enough to find that car," said Russell. "The known facts are possibly sufficient to enable one to discover the exact number. You see, there must be a limit to the five-figure numbers having the peculiarity observed by the simpleton. And these are further limited by the fact that, as Mrs. Wadey states, the number began with the figure 1. We have therefore to find these numbers. It may conceivably happen that there is only one such number, in which case the thing is solved. But even if there are several cases, the owner of the actual car may easily be found.

"How will you manage that?" somebody asked.

"Surely," replied Russell, "the method is quite obvious. By the process of elimination. Every owner except the one in fault will be able to prove an alibi. Yet, merely guessing offhand, I think it quite probable that there is only one number that fits the case. We shall see."

Russell was right, for that very night he sent the number by post, with the result that the runaway car was at once traced, and its owner, who was himself driving, had to pay the cost of the damages resulting from his carelessness. What was the number of the car?

65.—The Mystery of Ravensdene Park

The mystery of Ravensdene Park, which I will now present, was a tragic affair, as it involved the assassination of Mr. Cyril Hastings at his country house a short distance from London.

On February 17th, at 11 p.m., there was a heavy fall of snow, and though it lasted only half an hour, the ground was covered to a depth of several inches. Mr. Hastings had been spending the evening at the house of a neighbour, and left at midnight to walk home, taking the short route that lay through Ravensdene Park—that is, from D to A in the sketch-plan. But in the early morning he was found dead, at the point indicated by the star in our diagram, stabbed to the heart. All the seven gates were promptly closed, and the footprints in the snow examined. These were fortunately very distinct, and the police obtained the following facts:—

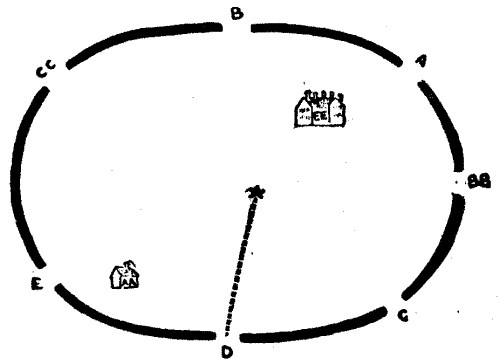
The footprints of Mr. Hastings were very clear, straight from D to the spot where he was found. There were the footprints of the Ravensdene butler—who retired to bed five minutes before midnight—from E to EE. There were the footprints of the gamekeeper from A to his lodge at AA. Other footprints showed that one individual had come in at gate B and left at gate BB, while another had entered by gate C and left at gate CC.

Only these five persons had entered the park since the fall of snow. Now, it was a very foggy night, and some of these pedestrians had consequently taken circuitous routes, but it was particularly noticed that no track ever crossed another track. Of this the police were absolutely certain, but they stupidly omitted to make a sketch of the various routes before the snow had melted and utterly effaced them.

The mystery was brought before the members of the Puzzle Club, who at once set themselves the task of solving it. Was it possible to discover who committed the crime? Was it the butler? Or the gamekeeper? Or the man who came in at B and went out at BB? Or the man who went in at C and left at CC? They provided themselves with diagrams—sketch-plans, like the one we have reproduced, which simplified the real form of Ravensdene Park without destroying the necessary conditions of the problem.

Our friends then proceeded to trace out the route of each person, in accordance with the positive statements of the police that we have given. It was soon evident that, as no path ever crossed another, some of the pedestrians must have lost their way considerably in the fog. But when the tracks were recorded in all possible ways, they had no difficulty in deciding on the assassin's route; and as the police luckily knew whose footprints this route represented, an arrest was made that led to the man's conviction.

Can our readers discover whether A, B, C, or E committed the deed? Just trace out the route of each of the four persons, and the key to the mystery will reveal itself.

66.—The Buried Treasure

The problem of the Buried Treasure was of quite a different character. A young fellow named Dawkins, just home from Australia, was introduced to the club by one of the members, in order that he might relate an extraordinary stroke of luck that he had experienced "down under," as the circumstances involved the solution of a poser that could not fail to interest all lovers of puzzle problems. After the club dinner, Dawkins was asked to tell his story, which he did, to the following effect:—

"I have told you, gentlemen, that I was very much down on my luck. I had gone out to Australia to try to retrieve my fortunes, but had met with no success, and the future was looking very dark. I was, in fact, beginning to feel desperate. One hot summer day I happened to be seated in a Melbourne wineshop, when two fellows entered, and engaged in conversation. They thought I was asleep, but I assure you I was very wide awake.

"'If only I could find the right field,' said one man, 'the treasure would be mine; and as the original owner left no heir, I have as much right to it as anybody else.'

"'How would you proceed?' asked the other.

"'Well, it is like this: The document that fell into my hands states clearly that the field is square, and that the treasure is buried in it at a point exactly two furlongs from one corner, three furlongs from the next corner, and four furlongs from the next corner to that. You see, the worst of it is that nearly all the fields in the district are square; and I doubt whether there are two of exactly the same size. If only I knew the size of the field I could soon discover it, and, by taking these simple measurements, quickly secure the treasure.'

"'But you would not know which corner to start from, nor which direction to go to the next corner.'

"'My dear chap, that only means eight spots at the most to dig over; and as the paper says that the treasure is three feet deep, you bet that wouldn't take me long.'

"Now, gentlemen," continued Dawkins, "I happen to be a bit of a mathematician; and hearing the conversation, I saw at once that for a spot to be exactly two, three, and four furlongs from successive corners of a square, the square must be of a particular area. You can't get such measurements to meet at one point in any square you choose. They can only happen in a field of one size, and that is just what these men never suspected. I will leave you the puzzle of working out just what that area is.

"Well, when I found the size of the field, I was not long in discovering the field itself, for the man had let out the district in the conversation. And I did not need to make the eight digs, for, as luck would have it, the third spot I tried was the right one. The treasure was a substantial sum, for it has brought me home and enabled me to start in a business that already shows signs of being a particularly lucrative one. I often smile when I think of that poor fellow going about for the rest of his life saying: 'If only I knew the size of the field!' while he has placed the treasure safe in my own possession. I tried to find the man, to make him some compensation anonymously, but without success. Perhaps he stood in little need of the money, while it has saved me from ruin."

Could the reader have discovered the required area of the field from those details overheard in the wineshop? It is an elegant little puzzle, and furnishes another example of the practical utility, on unexpected occasions, of a knowledge of the art of problem-solving.

THE PROFESSOR'S PUZZLES

"Why, here is the Professor!" exclaimed Grigsby. "We'll make him show us some new puzzles."

It was Christmas Eve, and the club was nearly deserted. Only Grigsby, Hawkhurst, and myself, of all the members, seemed to be detained in town over the season of mirth and mince-pies. The man, however, who had just entered was a welcome addition to our number. "The Professor of Puzzles," as we had nicknamed him, was very popular at the club, and when, as on the present occasion, things got a little slow, his arrival was a positive blessing.

He was a man of middle age, cheery and kind-hearted, but inclined to be cynical. He had all his life dabbled in puzzles, problems, and enigmas of every kind, and what the Professor didn't know about these matters was admittedly not worth knowing. His puzzles always had a charm of their own, and this was mainly because he was so happy in dishing them up in palatable form.

"You are the man of all others that we were hoping would drop in," said Hawkhurst. "Have you got anything new?"

"I have always something new," was the reply, uttered with feigned conceit—for the Professor was really a modest man—"I'm simply glutted with ideas."

"Where do you get all your notions?" I asked.

"Everywhere, anywhere, during all my waking moments. Indeed, two or three of my best puzzles have come to me in my dreams."

"Then all the good ideas are not used up?"

"Certainly not. And all the old puzzles are capable of improvement, embellishment, and extension. Take, for example, magic squares. These were constructed in India before the Christian era, and introduced into Europe about the fourteenth century, when they were supposed to possess certain magical properties that I am afraid they have since lost. Any child can arrange the numbers one to nine in a square that will add up fifteen in eight ways; but you will see it can be developed into quite a new problem if you use coins instead of numbers."

69.—The Frogs and Tumblers

"What do you think of these?"

The Professor brought from his capacious pockets a number of frogs, snails, lizards, and other creatures of Japanese manufacture—very grotesque in form and brilliant in colour. While we were looking at them he asked the waiter to place sixty-four tumblers on the club table. When these had been brought and arranged in the form of a square, as shown in the illustration, he placed eight of the little green frogs on the glasses as shown.

"Now," he said, "you see these tumblers form eight horizontal and eight vertical lines, and if you look at them diagonally (both ways) there are twenty-six other lines. If you run your eye along all these forty-two lines, you will find no two frogs are anywhere in a line.

"The puzzle is this. Three of the frogs are supposed to jump from their present position to three vacant glasses, so that in their new relative positions still no two frogs shall be in a line. What are the jumps made?"

"I suppose–" began Hawkhurst.

"I know what you are going to ask," anticipated the Professor. "No; the frogs do not exchange positions, but each of the three jumps to a glass that was not previously occupied."

"But surely there must be scores of solutions?" I said.

"I shall be very glad if you can find them," replied the Professor with a dry smile. "I only know of one—or rather two, counting a reversal, which occurs in consequence of the position being symmetrical."