
Вселенная! Курс выживания среди черных дыр. временных парадоксов, квантовой неопределенности
Иногда температура бывает выше среднего, иногда ниже. Если разброс достаточно велик, мы не замечаем небольших изменений от года до года. На самом деле нет ничего необычного в том, что температура стоит на 10° C выше среднего, как нет ничего необычного и в том, что она падает на 10° C ниже среднего. Что будет через год, когда в Филадельфии выдастся холодная зима и средняя температура в декабре будет –7° C? Тогда кузен Герман будет утверждать, что шум вокруг глобального потепления подняли зря, и снова примется мастерить свой шлем из фольги. Он не видит, в чем сложность, поскольку сосредоточен на отдельных днях, а не на тенденции. Ну и что? У вас на совести наверняка есть грешки и похуже.
Даже освободившись от тревог за кошмарное будущее планеты, Герман все равно найдет о чем тревожиться. Почему непонятные мелкие частички в его стакане с водой все кружатся и кружатся? Какова вероятность, что через двести лет в Землю врежется гигантский астероид? Долго ли проживет его ручной нейтрон? Возможно, раньше все это вас не заботило, но каждое из этих явлений – результат последовательности случайных событий в действии.
I. Если физический мир настолько непредсказуем, почему мы замечаем это далеко не всегда?
На отдаленной ветке генеалогического древа (и на пыльной дальней полке генофонда) находится дядя Луи. Он человек по-своему обаятельный – сыплет солеными шуточками и постоянно просит маленьких детишек дернуть его за палец. Племянники и племянницы дяди Луи заплатили за колледж монетками в четверть доллара, которые он натаскал из ушей. Однако дядя Луи – патологический азартный игрок. Дядя Луи готов заключать пари по поводу чего угодно – чем кончится фильм, кто победит в гонке раков-отшельников, ну и так далее. Поэтому дядя Луи и Дейв прячутся от тети Мейвис в туалете и играют там в старую добрую игру – бросают монетку. Ну что в этом плохого, скажите на милость, если только монетка не крапленая?
Чтобы понять суть игры, надо объяснить, что значит «некрапленая монетка». Если монетку кидали миллион раз, то решка будет выпадать примерно в половине раз. Чем дольше бросают монетку, тем ближе к 50 % будет частота решек. Кроме того, монетка «некрапленая», если каждый следующий бросок не зависит от предыдущего. Неважно, что выпало только что – орел или решка: в следующий раз с той же вероятностью в 50 % выпадет орел или решка.
Но вот в чем загвоздка. Хотя мы ожидаем, что после миллиона бросков дядя Луи и Дейв будут идти примерно ноздря в ноздрю, мы имеем в виду именно дроби.
Технический уголок дяди Дейва. Немного статистики
В начале книги мы пообещали вам следить, чтобы количество формул не превышало абсолютного минимума. Вот уже некоторое время мы придерживаемся правила «без формул», но при чтении такой математикоемкой главы, как эта, наверняка найдутся мазохисты, которые потребуют еще. «Откуда взялись эти числа?» – слышится ваш вопль. Поэтому вот вам еще капелька математики.
Когда дядя Луи бросает некрапленую монетку, существует, как мы упоминали, достаточно высокая вероятность, что решка будет выпадать примерно в половине раз. Насколько точно? Есть полезное правило: разброс результатов будет примерно равен квадратному корню из удвоенного ожидаемого количества решек (то есть «побед»). Для простоты мы немного сжульничали, но основную картину это не меняет. Так что если вы бросаете монетку миллион раз, то, скорее всего, получите решку полмиллиона раз плюс-минус 1000 раз.
Если Луи с Дейвом бросают монетку миллион раз, Луи может и выиграть много денег, и проиграть много денег, зато утешением ему станет мысль о том, что все равно он выигрывал почти 50 % раз. Если он выиграет 501 тысячу раз (на тысячу выигрышей больше половины), то все равно окажется, что он выигрывал всего 50,1 % раз. Это и в самом деле напрасная трата времени и не слишком надежный способ сорвать приличный куш (или проиграться в дым).
В полновесных долларах картина будет иной. После миллиона бросков весьма вероятно, что Дейв или дядя Луи выиграют примерно на тысячу раз больше половины и сорвут приличный куш (или наоборот). Если вам интересно, откуда взялось это число – 1000, – рекомендуем посетить «Технический уголок дяди Дейва». Если неинтересно, ничего страшного. Это не входит в обязательную литературу по предмету.
Нас должно радовать, что в наших силах предсказать вероятность едва ли не любого исхода. Например, в игре в миллион подбрасываний Луи (или Дейв) вправе ожидать различных результатов игры со следующими вероятностями:
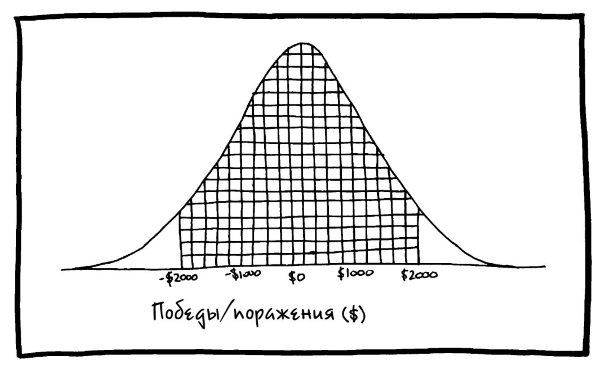
Чем выше кривая, тем вероятнее такой исход. Самый вероятный результат – это что они будут квиты, но Луи может выиграть (или проиграть) одну-две тысячи и при этом не слишком удивляться своему (не)везению. Хвостики по обеим сторонам графика означают, что крайне маловероятно, чтобы Дейв или дядя Луи выигрывали в подавляющем большинстве случаев. Однако, строго говоря, не исключено, что Луи бросит монетку миллион раз и каждый раз будет выпадать решка. С другой стороны, вероятность такого исхода так мала, что слово «микроскопический» рядом с ней кажется наглым преувеличением.
Если бы за везением Луи или Дейва в ходе игры следил математик, он бы описал их прогресс как «случайное блуждание». Чтобы понять, что это такое, найдите какой-нибудь неподвижный предмет, например фонарный столб. Теперь встаньте рядом с ним и бросьте монетку. Если выпадет решка, сделайте шаг на запад, а если выпадет орел – на восток. С течением времени вы с равной вероятностью окажетесь к востоку или к западу от столба, но при этом в среднем будете от него удаляться[45].
Вместо того чтобы просто описывать везение дяди Луи, мы докажем свою точку зрения тем, что просто сядем и подбросим монетку миллион раз. Ну, как дела у Луи?
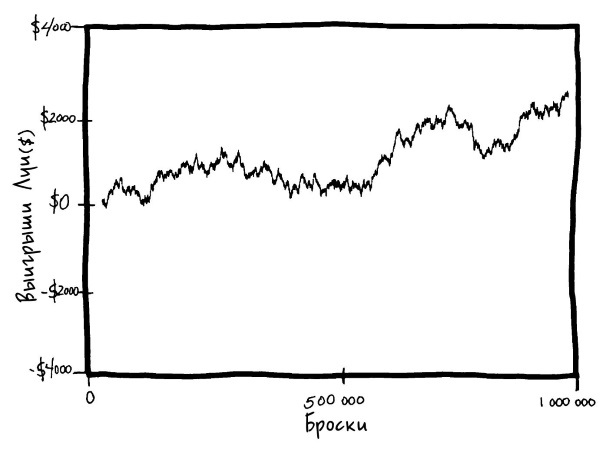
Только поглядите! Он выиграл у своего бедного, изнуренного интеллектуальным трудом племянника-студента целых 2000 долларов! Если вы посмотрите на то, как фортуна улыбалась Луи и как она от него отворачивалась, то наверняка заметите тенденции. Возможно, примерно в середине игры у Луи выдалась череда выигрышей. Дело не в том, что у него «крапленая» монетка, в которую со стороны решки впаян кусочек свинца, дело не в том, что Луи – закоренелый шулер. Это просто результат того, что ваш мозг видит закономерности там, где их нет. Если вы когда-нибудь вкладывали деньги в ценные бумаги, то, вероятно, наблюдали такие же закономерности, когда индекс промышленных акций Доу-Джонса вдруг в течение двух месяцев кряду держался выше среднего[46]
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Примечания
1
Когда миссис Голдберг прочитала рукопись, она наконец призналась, что на нашем первом свидании прикусила язык и титаническим усилием воли заставила себя не говорить ничего подобного.
2
На одной такой «юмористической» обложке были изображены кегли, разлетающиеся от мяча для боулинга, что, по мысли автора, символизировало студентов, пораженных мощью и размахом физической науки.
3
Хотя один из авторов утверждает, что все наши иллюстрации или остроумны, или познавательны, или и то и другое.
4
Заодно и дадим очередного пинка.
5
По крайней мере так гораздо проще для тех ученых, которые знают, что такое сверхтонкий переход. Вам этого знать не надо, на контрольной этого не будет.
6
По крайней мере в ближайшие 180 секунд.
7
Те из вас, кто особенно поднаторел в научной фантастике, вероятно, слышали о гипотетической частице под названием тахион, которая движется быстрее света. Такую частицу пока никто не поймал. Тахион как физическая частица, а не математическое понятие пока что принадлежит к области научной фантастики, а не наших интересов.
8
Если вы забыли, напомним, что это узелок в горошек, привязанный к палке.
9
Нет. В данном случае – нет. Но однажды он все-таки перемудрил. Об этом мы поговорим в главе 6.
10
«Мост над бурной рекой» (Bridge over Troubled Water) – знаменитый хит Саймона и Гарфункеля. – Примеч. перев.
11
Поняли, в чем соль?
12
ЧЕГО?!
13
Как и вероятность того, что Рыжий выйдет из своего вагона на планету, населенную сверхинтеллектуальными, подлыми, грязными обезьянами.
14
Зато вы пойдете домой с этой книгой в качестве утешительного приза. И никто, кроме вас, не узнает, какой вы мастер догадываться, если, конечно, не заглядывает сейчас в книгу вам через плечо.
15
Совсем наоборот! (фр.)
16
То есть над тем вопросом, который нам известен. Дети в этом возрасте такие почемучки…
17
Физики обожают напоминать, что при ядерных реакциях никакого горения не происходит. Горение – это не ядерный, а химический процесс, и для него нужен кислород.
18
«Идиот» по-клингонски. Не бейте нас тапком.
19
Если вы опустили глаза и обнаружили, что на вас пижама, значит, вам опять снится этот треклятый сон.
20
Примерно как прыщ перед выпускным балом.
21
Если вы не англичанин, он известен вам как офицер полиции.
22
Еще как понимают.
23
Вот, скажем, Халк («Фантастическая четверка») черпает силу не в рентгеновских, а в космических лучах, о которых мы поговорим в следующей главе.
24
Тот факт, что действиями в настоящем мы, оказывается, способны изменять прошлое, крушит не только мировоззрение, но и глагольные времена.
25
А фраза «посидеть дома одному в субботу вечером» дополнительных объяснений не требует. Сидите, невежды, дома и дочитывайте эту книгу, причем с радостью, кому сказано?!
26
Да, мы понимаем, что технически они одно и то же лицо. Вот это мы и называем метафорой.
27
Строго говоря, это не скорость, а импульс. Если вы уже разбираетесь в физике настолько, что понимаете, чем скорость отличается от импульса, значит, мы доверим вам высокую честь остаться на перемене в классе и вытереть доску.
28
Воистину этот человек – настоящее чудовище.
29
Если речь идет о Хайде – то врагу.
30
Когда физики так говорят, они имеют в виду «исчезающе малую» вероятность. А когда мы говорим «нетривиальный», то имеем в виду «почти невозможный».
31
«Признайтесь, Пойндекстер! У вас есть собственный унитард с отличительными знаками Звездного Флота!»
32
Как именно, мы расскажем в следующей главе.
33
Фанфары!
34
Чтобы расставить все точки над i, уточним, что эксперимент этот сугубо мысленный. Однако он наводит на самые печальные мысли относительно психического склада Шредингера.
35
Что, в свою очередь, позволяет нам лениться, а это мы любим…
36
Видите ли, когда он выдумывал эксперимент с котом в ящике, то как раз хотел поиздеваться над копенгагенской интерпретацией.
37
Надеемся, что вы, главный солипсист, это учтете.
38
Если вам кажется, что мы опять впали в демагогию, проверьте сами.
39
Роскошный сюжет для комикса. Рекомендуем.
40
У этой медали есть и обратная сторона. Наверняка кто-то из «вас» болтал по мобильнику в театре во время спектакля или запустил лапу в кружку для церковных пожертвований. После такого мы никогда не подадим вам руки.
41
Альфред Э. Ньюмен – популярный в США персонаж карикатур, придурковатый мальчишка, который вечно дожидается, когда сзади подкрадется жареный петух и… «А мне-то о чем беспокоиться?» – девиз всей его жизни. – Примеч. перев.
42
Если правы создатели музейных диарам, этот сценарий вполне оправдался для некоторых пещерных людей. Кто мы такие, чтобы сомневаться в этом?
43
В котором наверняка замешана Трехсторонняя комиссия. Как же без нее.
44
В частности, Межправительственный комитет по переменам климата. Звучит очень официально. Не сомневаемся, Герман это учтет.
45
Кроме того, вы рискуете оказаться посреди проезжей части, бросая в воздух мелочь. Такие опасные эксперименты лучше предоставить самим математикам.
46
Мы писали эти строки в начале 2009 года, когда рыночные тенденции в целом представляются определенно неслучайными.
Приобретайте полный текст книги у нашего партнера:

